Funções

Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação? 

Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.

Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂

Conceitos

O que dizer sobre funções? Bem, dizemos que funções são relações entre dois conjuntos, nas quais todos os elementos do primeiro estão associados unicamente a um elemento do segundo, nem mais, nem menos. No entanto, um elemento do segundo conjunto pode se relacionar com nenhum ou mais de um elemento do primeiro conjunto. Achou confuso? A figura a seguir ilustra essa definição:

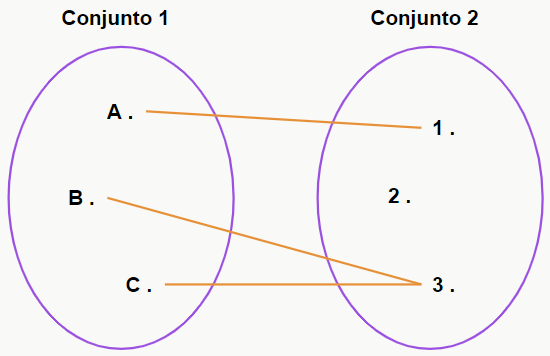
Uma maneira mais informal de definir funções é dizer que ela é uma espécie de fábrica, onde você “coloca” um ingrediente no início e “recebe” um produto no final, como mostrado na figura a seguir:

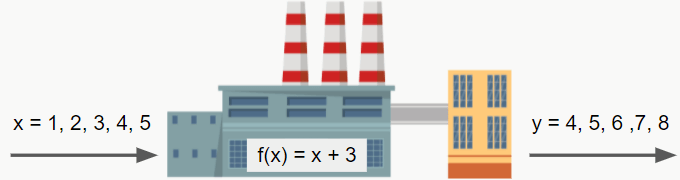
Perceba que, para representar a função, utilizamos a notação f(x), mas recebemos y como resultado, como pode isso? Isso acontece porque escrever f(x) = expressão é o mesmo que escrever y = expressão, pois f(x) = y. E o contrário também é verdade, f(y) = x. E por que especificamente x e y? Pois são os dois eixos do plano cartesiano bidimensional. Lembre-se que as funções são muito utilizadas para a construção de gráficos. Além disso, as funções são utilizadas para modelar fenômenos reais, ou seja, representar matematicamente fenômenos cotidianos, possibilitando que possamos prever o futuro… 😵

Mas como reconhecer e representar uma função?

1- Já vimos isso no começo, né? Mas relembrando, para dizer que uma expressão matemática é uma função, usa-se a notação f(variável), como por exemplo, f(x), que significa que a expressão é uma função de x, ou seja, é uma expressão que depende de x. Por enquanto você só verá funções com 1 variável, mas saiba que existem funções com 2, 3 e até mais variáveis. 😮

2- Na linguagem matemática, funções são representadas da seguinte forma: f : A → B, ou, no português, “f de A em B”, onde f é nossa expressão matemática (a função); A é o domínio da função; e B é o contradomínio.

Mas o que são essas coisas? Vamos dar uma espiada nesses e em alguns outros conceitos importantes.

Domínio, Contradomínio e Imagem

O domínio de uma função matemática diz respeito a todos os valores que podem substituir a incógnita em uma expressão. Ou seja, na hora de substituir o “x” por um número qualquer, você só pode utilizar os que fizerem parte do domínio da função.

A imagem de uma função é simplesmente o resultado obtido após cada operação, e como vimos anteriormente na definição de funções, cada número pertencente ao domínio da função só pode ter um único resultado como imagem. No entanto, um mesmo valor de imagem pode ser obtido por mais de um valor do domínio. Vemos então que todo elemento do conjunto imagem está obrigatoriamente associado a um elemento do domínio.

Já o contradomínio de uma função diz respeito a um conjunto numérico que abranja no mínimo os elementos que fazem parte da imagem da função. A diferença deste conjunto para a imagem é que nem todos os valores presentes no contradomínio precisam se relacionar com elementos do domínio, ou seja, nem todos os valores contidos no contradomínio precisam aparecer como resultado da expressão. Desse modo, dizemos que a imagem é um subconjunto do contradomínio.

Difícil? Vamos dar uma olhada em alguns exemplos que vão te ajudar a entender melhor e fixar os conceitos.

Lembra da notação apresentada anteriormente? Então partiu utilizá-la:

Ex 1: f : I → N, sendo f(x) = x²

Observe que o domínio da função é o conjunto dos números inteiros, porém, como qualquer número elevado ao quadrado resultará em um valor positivo, desse modo, optei por ter o conjunto dos números naturais como contradomínio, pois ele abrange todos os possíveis valores resultantes da expressão. Nesse caso, você poderia optar também por utilizar os conjuntos dos números inteiros ou reais como contradomínio, pois todos esses contém a imagem da expressão.

Mas não é sempre que isso acontece, seguimos para mais um exemplo.

Ex 2: f : I → R, sendo f(x) = x³

Neste caso, o domínio da função continua sendo o conjunto dos números inteiros, porém, o contradomínio é o conjunto dos números reais, pois no caso dessa expressão, podemos encontrar números negativos na imagem. Mas poderíamos indicar os números inteiros como contradomínio? A resposta é: sim, pois conteria tanto números positivos quanto negativos. E os naturais? Nesse caso, não. Note que o conjunto dos números naturais não engloba os números negativos, portanto, não estaríamos seguindo a regra de abranger no mínimo os valores da imagem.

E agora, ficou mais claro o que é domínio, contradomínio e imagem? Antes de finalmente olharmos para as funções estudadas no Ensino Médio, vamos rapidamente definir alguns nomes especiais que elas podem receber.

Propriedades das funções

• Função sobrejetora: neste caso especial, temos que o contradomínio é exatamente igual à imagem, ou seja, todos os elementos do contradomínio estão associados a um elemento do domínio.

• Função injetora: neste segundo caso, cada elemento da imagem está associado a somente um único elemento do domínio, ou seja, dois números diferentes nunca resultam na mesma resposta.

• Função bijetora: neste terceiro caso, a função é sobrejetora e bijetora ao mesmo tempo, ou seja, o contradomínio é igual à imagem e dois números diferentes nunca resultam na mesma resposta.

Ufa! Depois de tantos conceitos, vamos finalmente dar uma olhada nas funções que aparecem durante o E.M.