Estudo de cônicas
Cônicas são figuras geométricas formadas a partir do chamado cone duplo de revolução, que consiste, de maneira bem informal, em “dois cones retos ligados verticalmente pelo vértice”, como ilustra a figura a seguir. Para obter as cônicas, é necessário fazer alguns “cortes” nesse cone, como veremos adiante. Fazendo isso, obtemos as seguintes figuras: elipse, hipérbole, parábola e circunferência.
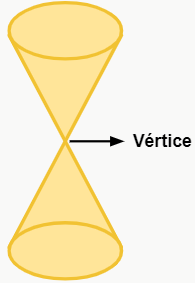
Hipérbole
A hipérbole é uma figura formada por duas curvas geradas a partir de um corte reto que passa pela base do cone, como mostra a figura a seguir:

Colocando a hipérbole em um plano, podemos destacar alguns pontos importantes da figura.
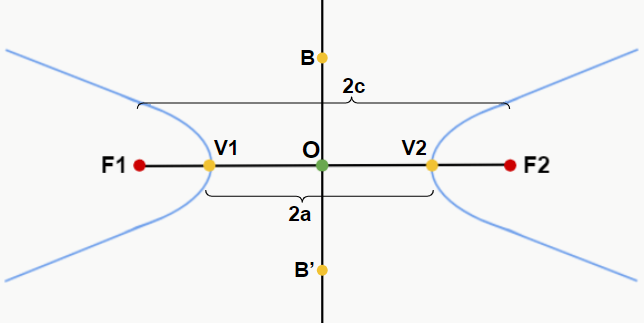
Onde F1 e F2 são os focos da hipérbole, V1 e V2 são os vértices da hipérbole, 2a é a distância entre os vértices (chamado de eixo real), 2c é a distância entre os focos, O é o centro da hipérbole e o eixo que contém os pontos B e B’ é chamado de eixo imaginário. A distância entre B e B’ é 2b.
Mas qualquer figura parecida com essa é uma hipérbole? A resposta é: Não! Para ser uma hipérbole, a figura deve respeitar a seguinte condição:
|d(PF1) – d(PF2)| = 2a
Ou seja, o módulo da distância de um ponto P da hipérbole até o foco F1 menos a distância desse mesmo ponto P até o foco F2 deve ser igual à 2a, que é a distância entre os vértices.
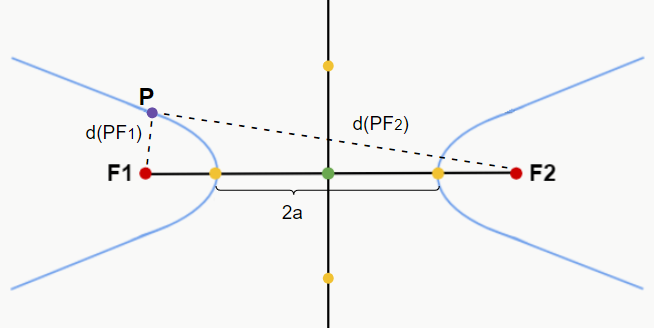
Um outro detalhe sobre a hipérbole é o fato de que podemos formar um triângulo retângulo utilizando os segmentos OB, OV2 e BV2. Note que este mesmo triângulo pode ser formado nas outras partes da hipérbole. Mas qual a importância disso? Observe as figuras a seguir:
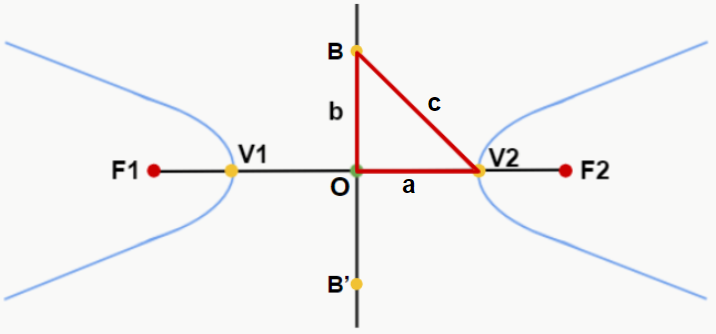
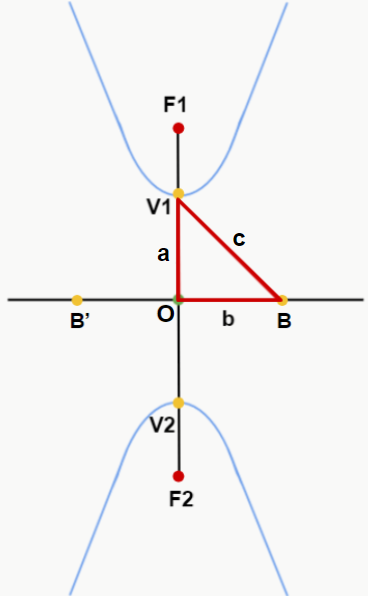
Note que a medida c, que agora representa a hipotenusa do triângulo retângulo OBV2 (ou OBV1) é o mesmo c da distância entre os focos. Portanto, concorda que c corresponde à distância entre o centro O e os focos F1 ou F2? Esse fato pode nos ajudar a resolver alguns problemas mais facilmente, pois como o triângulo é retângulo, podemos utilizar o Teorema de Pitágoras para encontrar a, b e c (c2 = a2 + b2).
Agora que já vimos todos os pontos importantes, vamos ver como é a equação da hipérbole. Perceba que há uma pequena diferença na equação quando os focos da hipérbole estão sobre o eixo x e quando eles estão sobre o eixo y.
Sobre o eixo x:
Sobre o eixo y:
Nessas equações, a é a distância entre o centro e um dos vértices, b é a distância entre o centro e um dos pontos imaginários (B ou B’) e x e y são quaisquer coordenadas da figura.
Já imaginou como seria construir no papel uma hipérbole que respeite todas as condições apresentadas nesta página? Isso é possível, e para tanto precisamos apenas de uma régua, de um barbante e algo para escrever. Veja o vídeo a seguir.
Acabamos por aqui o estudo da hipérbole, porém ainda precisamos falar sobre uma das cônicas mais famosas da matemática, a parábola!