Sistemas Lineares
Sistemas lineares são conjuntos de equações associadas entre si e que possuem duas ou mais variáveis. Em sistemas lineares, entram apenas equações lineares, ou seja, expressões onde o maior expoente das incógnitas é igual a 1.
Selecione aqui o conteúdo que deseja ver!
Método de solução: escalonamento
Este método de solução consiste em utilizar as operações básicas da matemática para transformar sistemas complicados em sistemas mais simples de serem resolvidos. Desse modo, podemos realizar as seguintes operações:
- Somar ou subtrair duas equações;
- Multiplicar as equações por números reais;
- Dividir as equações por números reais diferentes de 0;
- Multiplicar ou dividir por números reais e depois somar ou subtrair as equações.
Contudo, não necessariamente você precisa executar cada uma dessas operações, pois isso varia de caso a caso. Para ficar mais fácil de entender como utilizar o escalonamento, vamos ver alguns exemplos.
Ex. 1: vamos utilizar o mesmo sistema SPD da página anterior.
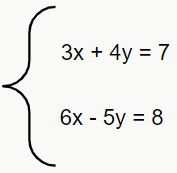
No escalonamento, existe mais de uma forma de resolver um sistema. Aqui faremos de um jeito, mas você pode tentar resolver de outras formas e ver se chega no mesmo resultado.
Vamos começar excluindo uma das variáveis. No nosso caso, vamos começar com a y. A fim de retirar a variável do sistema, vamos multiplicar a primeira equação por 5 (coeficiente de y na equação 2), e a segunda equação por 4 (coeficiente de y na equação 1).
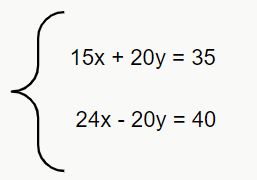
Agora temos que somar as equações. Perceba que a variável y some, pois 20y – 20y = 0.
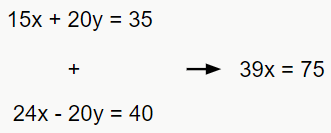
Para encontrar o valor de x, basta isolá-lo na equação. Feito isso, é só substituir o valor encontrado em qualquer uma das equações iniciais para encontrar o valor de y.
Portanto, encontramos x = 25/13 e y = 4/13. Se você substituir esses valores nas equações, verá que elas satisfazem ambas as expressões.
Ex. 2:
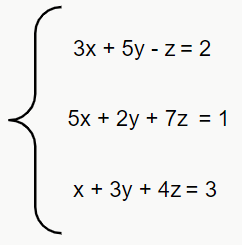
Agora temos 3 variáveis, o que torna nossa solução um pouco mais complicada. Novamente, não há somente um modo de resolver esse sistema pelo método do escalonamento, então você pode tentar resolvê-lo de outra forma se quiser. Sendo assim, vamos ver o que podemos fazer.
Sugiro que primeiro tentemos eliminar alguma variável de uma das expressões. Que tal a variável x? Vamos então pegar a terceira expressão, multiplicar por -3 e somar com a primeira equação para eliminar a variável.
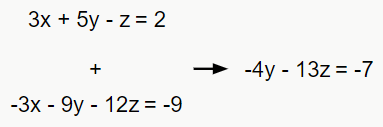
Agora temos uma nova expressão com apenas duas variáveis, o que fazer então? Percebe que podemos isolar uma delas. Nesse caso, vou escolher isolar o y.
Tendo y em função de z, podemos substituir y pela expressão acima em qualquer uma das equações iniciais, e isso vai nos deixar com apenas 2 variáveis. E já sabemos como trabalhar com duas variáveis, certo?
Desse modo, vamos substituir y na primeira expressão:
O que fazer agora? Vamos isolar uma das incógnitas. Como já temos y em função de z, é recomendável colocar o x também em função de z. Consegue visualizar onde queremos chegar?
Agora que temos tudo em função de z, vamos escolher uma equação e substituir todas as expressões que encontramos. Dessa forma, teremos uma equação composta somente pela variável z, nos permitindo encontrar seu valor. Escolho a terceira equação.
Isolando a variável, encontramos que z = 9/13. Lembra das nossas equações em que tínhamos x e y em função de z? Então, agora é só substituir o valor de z e encontrar o valor das outras variáveis.
Fazendo isso, encontramos que x = 45/26 e y = -1/2. Se você substituir esses valores nas equações, verá que eles realmente satisfazem as expressões.
Todo esse processo é bem trabalhoso, né? Será que não tem um jeito mais fácil? A resposta é: tem sim, a chamada Regra de Cramer.