Circunferência e Círculo
Circunferências e círculos são figuras planas bem comuns no cotidiano. Quem nunca viu um bambolê, um anel, um relógio ou uma roda de bicicleta? Desse modo, é importante saber como diferenciá-las e como calcular algumas informações importantes, como área, perímetro, comprimento de arcos, além de entender como utilizar os ângulos presentes no círculo. É… esse assunto tem mais coisas do que você pensou, né? Vamos estudá-lo então?
Selecione aqui o conteúdo que deseja ver!
Trigonometria na circunferência
Na página sobre triângulos falamos sobre trigonometria e sobre as relações trigonométricas, você lembra quais são elas? O que importa para nós agora é que podemos aplicar essas mesmas relações em uma circunferência e, consequentemente, ampliar ainda mais nossos estudos sobre trigonometria. Veja a figura a seguir:
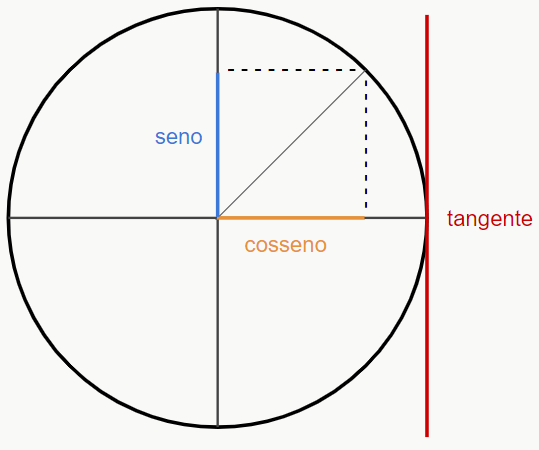
Note que nela estão todas as relações que vimos na página sobre trigonometria no triângulo retângulo: seno, cosseno e tangente. Perceba também que o eixo x (abscissas) representa o cosseno, enquanto o eixo y (ordenadas) representa o seno. Guarde essa informação, pois ela será muito valiosa quando falarmos dos ângulos. 😉 Mas dá para encaixar os ângulos aí também? Sim, uma volta completa pela circunferência é igual a 360° (graus) ou 2pi radianos, como podemos verificar na imagem a seguir.
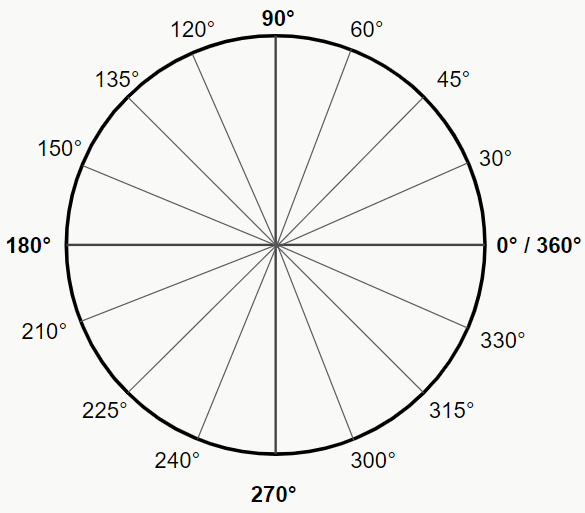
E cada um desses ângulo possui seus próprios valores das razões trigonométricas. Nossa, mas mesmo se contarmos apenas os ângulos da figura, são muitos, como vou lembrar dos valores de tudo isso? A verdade é que, sabendo o valor dos ângulos notáveis e lembrando qual eixo representa o seno e qual representa o cosseno, sua vida vai ficar muito mais fácil, mas… antes de eu te mostrar o porquê, precisamos ver mais uma coisinha.
Os quadrantes da circunferência
A circunferência trigonométrica pode ser dividida em 4 quadrantes, ou seja, quatro regiões de mesmo tamanho, conforme a figura a seguir:
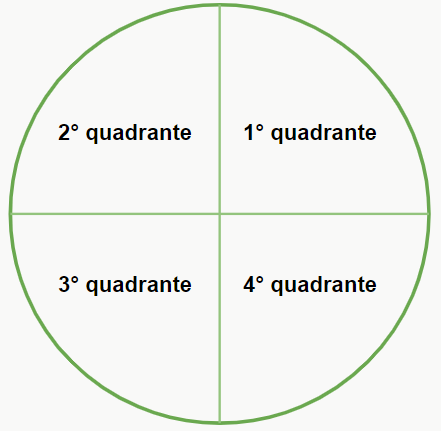
Note que, se elas possuem o mesmo tamanho e sabemos que os ângulo vão de 0° a 360°, então cada quadrante “abriga” 90°, correto? Sendo assim, temos que:
1° quadrante = entre 0° e 90°
2° quadrante = entre 90° e 180°
3° quadrante = entre 180° e 270°
4° quadrante = entre 270° e 360°
Note que a palavra “entre” foi utilizada para designar os ângulos de cada quadrante. Isso significa que os ângulos 0°, 90°, 180°, 270° e 360° não fazem parte dos quadrantes, estando posicionados sobre os eixos x e y.
Outro ponto importante sobre os quadrantes é que os sinais – positivo (+) ou negativo (–) – do seno, cosseno e tangente, irão variar de acordo com o ângulo que temos em mãos. E essa variação está expressa na imagem e quadro a seguir.
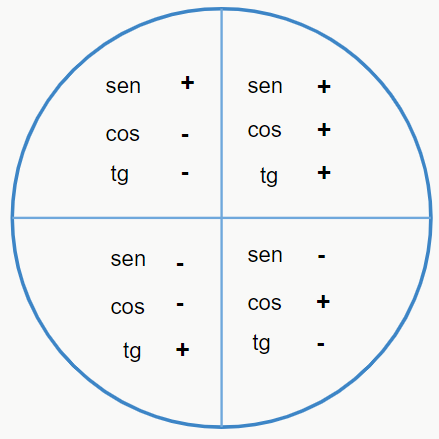
| 1° quadrante | 2° quadrante | 3° quadrante | 4° quadrante | |
| Seno | + | + | – | – |
| Cosseno | + | – | – | + |
| Tangente | + | – | + | – |
Mas por que isso é importante? Lembra que foi dito anteriormente que não é necessário decorar o valor das relações trigonométricas de todos os ângulos presentes na segunda figura da página? Então, isso não é necessário justamente porque os valores de seno, cosseno e tangente são iguais em todos os quadrantes, o que vai mudar é somente o sinal da relação. Observe as figuras a seguir:
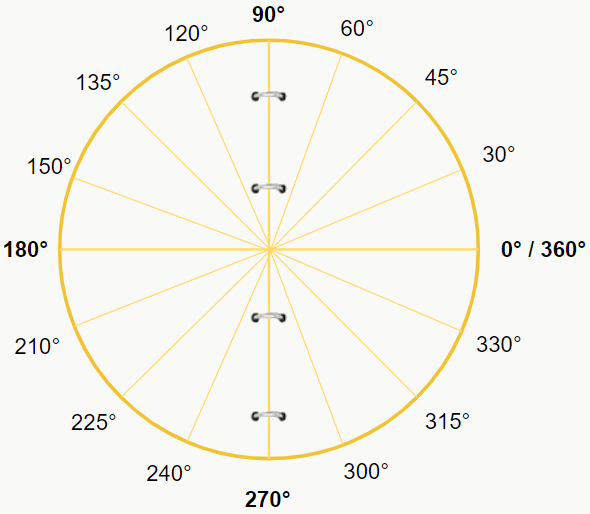
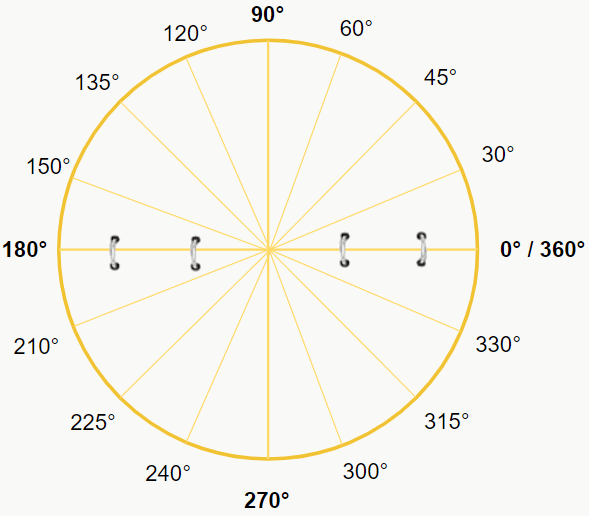
Nas circunferências foram colocados arames circulares nos eixos x e y (igual aos que tem nos cadernos e livros) que nos permitem “virar“ os quadrantes. Perceba que, independente do quadrante que você tentar movimentar (faça esse exercício mental), ele sempre estará completamente sobre o outro, e isso acontece pois a figura é uma circunferência, que é simétrica. Desse modo, temos que, ao movimentar o quadrante 1 em direção ao 2, temos que o ângulo de 60° fica sobre 120°, 45° fica sobre 135° e 30° fica sobre 150°. E isso vale para qualquer movimento que tentar fazer, sempre teremos ângulos que “sobrepõem” outros. E o que isso nos diz? Isso nos diz que esses ângulos que se “sobrepõem” possuem os mesmos valores de seno, cosseno e tangente, e a única coisa que vai mudar de um para outro é o sinal correspondente a seus respectivos quadrantes.
Mas não precisa ficar fazendo esse exercício mental toda vez que quiser saber se o ângulo de um quadrante possui os mesmos valores de outro. Para isso, tomando como base os ângulos agudos (menores que 90°), basta seguir uma regra bem simples, que consiste em subtrair o ângulo desejado dos valores 180° e 360°.
Exemplo: escreva os valores de seno, cosseno e tangente dos ângulos a) 120°, b) 225° e c) 300°.
a) Seguindo a regra, fazemos 180 – 120 = 60
Portanto, 120° terá os mesmos valores que 60°, agora temos que verificar os sinais. Como 90 < 120 < 180, então vemos que o ângulo faz parte do segundo quadrante.
b) 225 – 180 = 45
Portanto, 225° terá os mesmos valores de 45°. Como 180 < 225 < 270, então vemos que o ângulo faz parte do terceiro quadrante.
c) 360 – 300 = 60
Portanto, 300° terá os mesmos valores de 60°. Como 270 < 300 < 360, então vemos que o ângulo faz parte do quarto quadrante.
Viu como é simples? Agora você sabe calcular as relações trigonométricas de qualquer ângulo. Mas e para os ângulos que estão nos eixos de simetria, como o 0°, 90°, 180°, 270° e 360°? Aí que entra a parte de saber onde fica o seno, o cosseno e a tangente na circunferência. Vamos relembrar a figura:
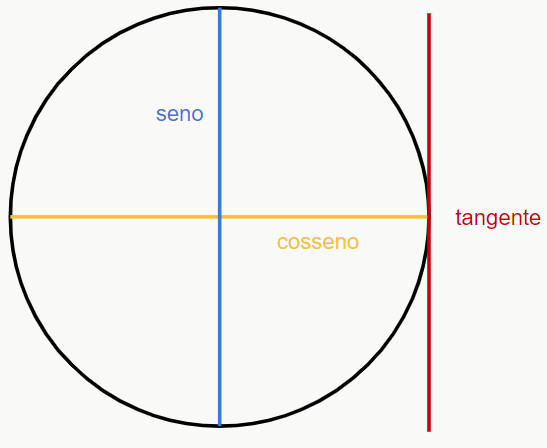
O eixo x é o do cosseno, o eixo y é o do seno, e a tangente é a linha vertical paralela ao eixo y. Como isso nos ajuda? Olha só, 0°, 180° e 360° fazem parte do eixo x (cosseno), então por isso, terão cosseno de módulo 1, faz sentido, né? Porém, 0° e 360° estão na parte positiva do eixo, enquanto 180° está na parte negativa, logo, cosseno de 0° e 360° = 1, enquanto cosseno de 180° = -1. E o seno? É 0 para todos, já que eles não fazem parte do eixo y (seno). E a tangente? Lembra que tangente é seno/cosseno? Então, 0/1 = 0, portanto, a tangente também é 0 para os três ângulos.
Entendeu a lógica? Vamos fazer o mesmo para 90° e 270°. Esses ângulos fazem parte do eixo y (seno), então possuem o módulo do seno igual a 1. Porém, 90° está na parte positiva, enquanto 270° está na parte negativa, ou seja, seno de 90° = 1 e seno de 270° = -1. E o cosseno? Ora, como eles não estão no eixo do cosseno, é 0. E a tangente? Fazendo seno/cosseno temos 1/0, e opa, não podemos dividir nada por 0. Portanto, não existe tangente de 90° e 270°.
Vamos agora organizar todos esses dados em uma tabela. O ideal é que você entenda a lógica desses resultados, pois entendê-la e aplicá-la é mais efetivo que simplesmente decorar os valores.
| Seno | Cosseno | Tangente | |
| 0° | 0 | 1 | 0 |
| 90° | 1 | 0 | não existe |
| 180° | 0 | -1 | 0 |
| 270° | -1 | 0 | não existe |
| 360° | 0 | 1 | 0 |
Para finalizar o assunto, vamos ver mais um pouquinho sobre ângulos?