Sistemas Lineares

Sistemas lineares são conjuntos de equações associadas entre si e que possuem duas ou mais variáveis. Em sistemas lineares, entram apenas equações lineares, ou seja, expressões onde o maior expoente das incógnitas é igual a 1.

Formato e classificações

Um sistema de equações lineares é representado da seguinte forma:

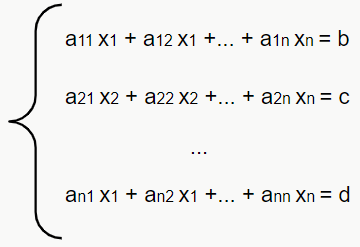
Ou seja, as equações que fazem parte do sistema são colocadas em linhas diferentes, e a chave é utilizada para mostrar que elas fazem parte do mesmo conjunto. Normalmente, para facilitar a visualização do sistema, colocamos incógnitas iguais sempre na mesma “coluna”, mas isso não é regra. Exemplo:

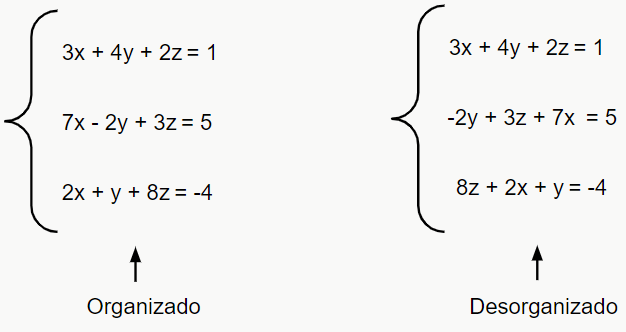
Veja como se torna muito mais fácil de entender o sistema quando deixamos ele organizado. 😉

Outro ponto importante dos sistemas lineares é em relação ao número possível de soluções que podemos encontrar. Para isso, eles recebem algumas classificações:

• Sistema Possível e Determinado (SPD): há apenas uma solução possível para o sistema. Para isso, o determinante principal do sistema deve ser diferente de 0. 

• Sistema Possível e Indeterminado (SPI): há infinitas soluções para o sistema. Para isso, o determinante principal do sistema deve ser igual a 0, e os determinantes secundários devem ser iguais a 0.

• Sistema Impossível (SI): não há soluções para o sistema. Para isso, o determinante principal deve ser igual a 0, e pelo menos um determinante secundário deve ser diferente de 0. 

Caso você ainda não saiba como calcular o determinante de uma matriz, acesse a página sobre o assunto e volte aqui depois, é rapidinho e você vai aprender bastante!

Mas se precisamos encontrar o determinante para classificar nosso sistema, isso significa que precisamos de uma matriz. E como se constrói uma matriz de um sistema linear?

Matriz de um sistema linear

Existem dois tipos de matrizes formadas a partir de um sistema de equações lineares. Utilizando o sistema a seguir, vamos construir os dois:

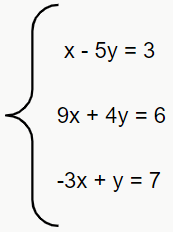
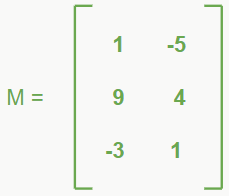
– Matriz incompleta

Essa matriz é formada apenas pelos coeficientes das incógnitas do sistema.

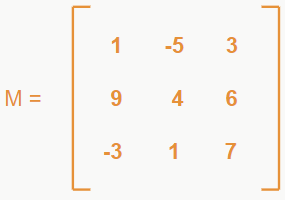
– Matriz completa

Essa matriz é formada tanto pelos coeficientes das incógnitas quanto pelos termos isolados do sistema (os que não acompanham nenhuma incógnita).

Bem tranquilo, né? Antes de resolvermos alguns exemplos, vamos só ver mais dois conceitos importantes.

Tipos de determinante de um sistema linear

Observe o seguinte sistema de equações:

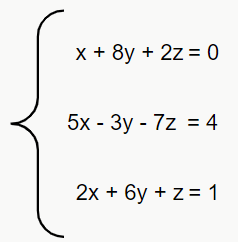
– Determinante principal

O determinante principal de um sistema linear será encontrado a partir da matriz formada apenas pelos coeficientes das incógnitas do sistema. Para o sistema acima, temos o seguinte determinante principal:

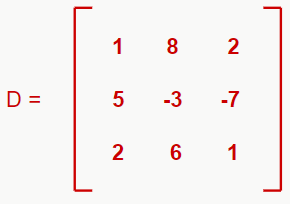
– Determinante secundário

Os determinantes secundários são aqueles relacionados a cada uma das incógnitas. Para encontrá-los, pegamos a matriz do determinante principal e trocamos os valores das colunas das respectivas incógnitas pelos valores dos termos isolados. Para o sistema acima, temos os seguintes determinantes secundários:

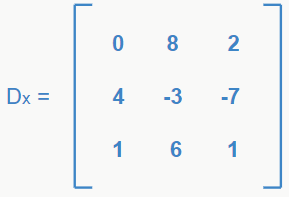
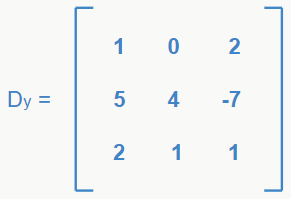
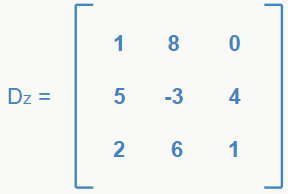
Pronto, agora que sabemos de todos os conceitos necessários, podemos finalmente partir para alguns exemplos e classificar nossos sistemas.

Ex. 1:

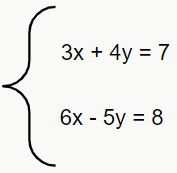
Com o sistema em mãos, temos que calcular o determinante principal.

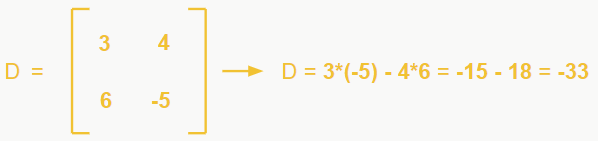
Portanto, como o determinante é diferente de 0, o sistema é SPD.

Ex. 2:

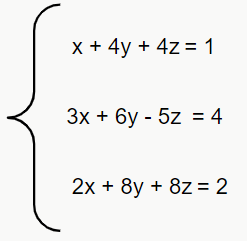
Vamos calcular o determinante.

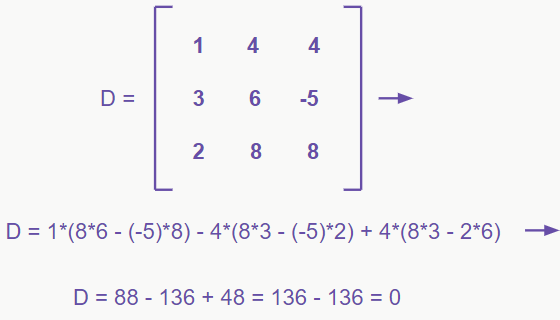
O determinante é 0, então já sabemos que o sistema não é SPD. No entanto, precisamos calcular pelo menos um determinante secundário para verificar se é SPI ou SI. Vamos calcular o determinante secundário da variável x.

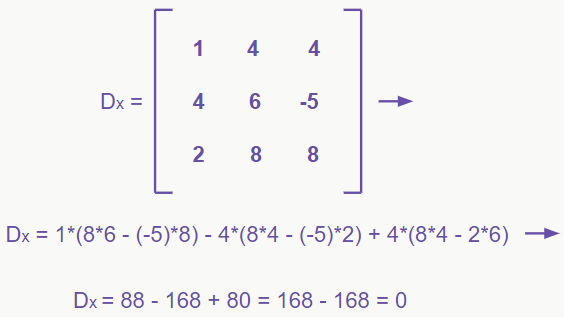
Portanto, como um dos determinantes secundários (D_x no caso), também é 0, podemos concluir que o sistema é SPI.

Aplicações de sistemas lineares

2) O GPS sem dúvidas é uma das aplicações mais importantes dos sistemas lineares, porém não é a única, já que o conteúdo é bastante utilizado na matemática, principalmente na geometria analítica. Existem ainda algumas outras aplicações desse conteúdo, porém são um pouco mais específicas. Caso tenha curiosidade, essas aplicações podem ser encontradas em: http://www.ime.unicamp.br/~apmat/sistemas-lineares-algumas-aplicacoes/

Referências