Circunferência e Círculo

Circunferências e círculos são figuras planas bem comuns no cotidiano. Quem nunca viu um bambolê, um anel, um relógio ou uma roda de bicicleta? Desse modo, é importante saber como diferenciá-las e como calcular algumas informações importantes, como área, perímetro, comprimento de arcos, além de entender como utilizar os ângulos presentes no círculo. É… esse assunto tem mais coisas do que você pensou, né? Vamos estudá-lo então?

Selecione aqui o conteúdo que deseja ver!

Circunferência e círculo

Arcos da circunferência

Trigonometria na circunferência

Ângulos côngruos e expressões

A circunferência

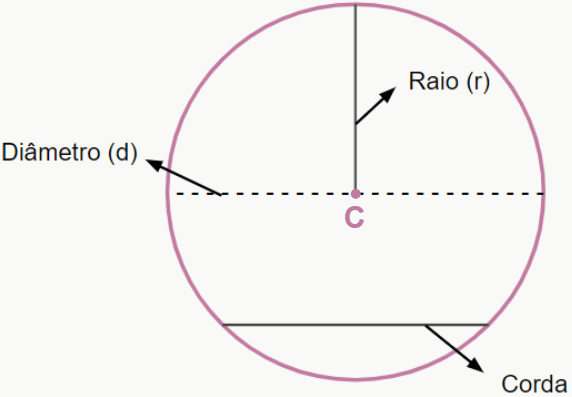
De modo formal, dizemos que a circunferência é um conjunto de pontos que possuem a mesma distância (equidistantes) de um determinado ponto central C. Como assim? Vamos olhar para a figura a seguir para entender melhor.

O ponto C é o centro da figura, e a “bordinha” é o que chamamos de circunferência. Veja que podemos colocar uma reta R entre o ponto C e a borda, e se girarmos essa reta R em qualquer sentido da circunferência, concorda que ela não muda de tamanho? Isso acontece justamente porque todos os pontos que formam nossa “bordinha” estão à mesma distância do ponto central. A essa reta R, daremos o nome de raio da circunferência.

Já sabemos o que é o raio da circunferência, mas existem outros elementos importantes que fazem parte desta figura, e são eles:

Diâmetro: o diâmetro é definido como sendo o segmento de reta que passa pelo ponto central C e une duas extremidades da circunferência. Perceba que o raio faz metade desse trabalho, pois liga o ponto C a uma extremidade, ou seja, o diâmetro pode ser calculado ao multiplicarmos por dois o valor do raio:

\[ d = 2*r \]

Da mesma forma, o raio pode ser calculado dividindo o diâmetro por dois (basta isolar r na equação anterior):

\[ r = \frac{d}{2} \]

Corda: a corda também é um segmento de reta que une dois pontos da circunferência, porém, este segmento não passa pelo centro, sendo essa a principal diferença para o diâmetro.

Perímetro (ou comprimento) da circunferência

Quando falamos de perímetro na página sobre polígonos, vimos que essa medida consiste na soma de todos os lados de uma figura. Contudo, quantos lados há em uma circunferência? É uma boa pergunta, mas na verdade a circunferência não tem lados. Dessa forma, para descobrir o perímetro (ou comprimento) de uma circunferência, temos que pegar a figura, fazer um “corte” nela e esticá-la, de modo a formar uma reta. Mas como determinar o tamanho dessa reta, tem que medir com a régua? É sempre uma possibilidade, mas há um jeito muito mais interessante de fazer isso. Sendo assim, a melhor forma de encontrar essa medida é utilizando a fórmula do comprimento da circunferência:

\[ C = 2*π*r \]

Exemplo: calcule o comprimento de uma circunferência com 10 cm de diâmetro. Utilize π = 3,14.

A fórmula nos pede o valor do raio, portanto precisamos lembrar que o valor do diâmetro é duas vezes o valor do raio. Desse modo, temos que raio = 5.

Agora é só substituir na fórmula do comprimento:

C = 2*3,14*5

C = 31,4 cm

Mas o que é esse π(pi) na fórmula?

O π (pi) é um número bem importante quando falamos de qualquer coisa relacionada a figuras circulares. Isso porque o número esse número pode ser encontrado sempre que dividimos o comprimento da circunferência pelo seu diâmetro, ou seja:

\[ π = \frac{c}{d} \]

E faz sentido, né? Como c = 2 * π * r e d = 2* r, temos que:

\[ π*2*r = π*2*r \]

Ou seja, a fórmula é verdadeira.

O pi, que é um número irracional, tem o valor de 3,14159265358979323846…, ou seja, é infinito, mas normalmente utilizamos somente o 3,14. Claro que quanto maior o número de casas decimais, mais preciso é o cálculo, mas duas casas decimais está bom demais para nós.

O número foi descoberto por Arquimedes, e por isso um de seus nomes é “Constante de Arquimedes”. Contudo, em 1707, o matemático inglês William Jones introduziu a letra grega π (pi) para representar o número 3,14…

O número é tão importante que tem até um dia no ano em homenagem a ele, arrisca dizer qual é? A resposta é 14/3, que vou deixar para você pensar o porquê de terem escolhido especificamente esse dia. 😉

Agora que já sabemos tudo sobre circunferência, que tal ver onde encontrá-la?

Por fim, outra forma de definir a circunferência é dizer que ela é a borda do círculo. Mas qual é a definição de círculo? É isso que veremos agora.

O círculo

O círculo é a região interna da circunferência, ou seja, se dizemos que a circunferência é a “borda” do círculo, isso significa que o círculo é o preenchimento da circunferência. Veja a figura a seguir:

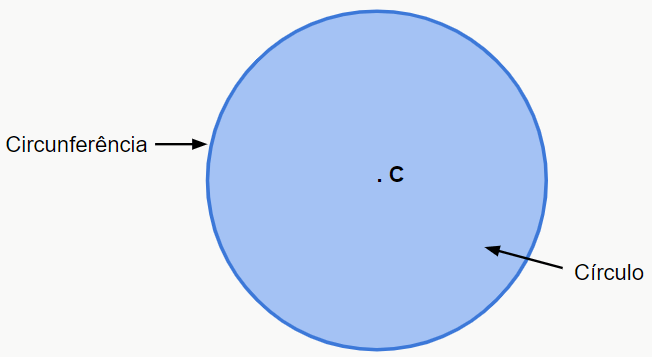
Os elementos que compõem o círculo são os mesmos que vimos na circunferência, ou seja, raio, diâmetro e corda. Contudo, o círculo não possui perímetro, pois não é uma “linha”, mas sim uma região do plano bidimensional. Desse modo, podemos calcular sua área com a seguinte fórmula:

\[ A = π*r^{2} \]

Exemplo: calcule a área de um círculo de raio 3 cm. Utilize π = 3,14.

Basta substituir na fórmula, né? Então vamos lá:

A = 3,14*3²

A = 3,14*9

A = 28,26 cm²

Que tal dar uma olhada em onde encontrar essa figura?