Polígonos

Polígonos são figuras fechadas formadas a partir de retas, ou seja, se a figura tiver uma curvinha que seja, não é um polígono. Existe uma enorme variedade de polígonos, e muitos deles podem ser observados no dia a dia. A palavra “polígono”, assim como diversas outras, é mais uma das nomenclaturas da matemática que tem origem grega: “poly” = “muitos”, e “gon” = “ângulos”, ou seja, polígono significa “muitos ângulos”. Mas tem muito mais que isso, vamos ver?

Selecione aqui o conteúdo que deseja ver!

Conceitos

Nomenclatura dos polígonos

Área e perímetro de polígonos

O perímetro de uma figura é definido pela soma de todos os seus lados. Exemplo: vamos calcular o perímetro das seguintes figuras.

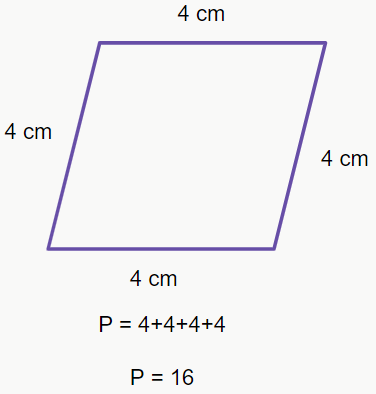
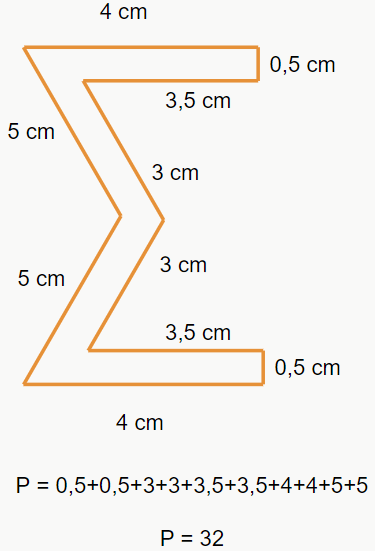
A área de uma figura plana corresponde à medida de sua superfície. De modo geral, o cálculo da área de polígonos regulares consiste em dividir a figura em diversos triângulos, calcular a área desses triângulos e depois multiplicar pela quantidade de triângulos que formam o polígono. Para o cálculo da área de quadrados e retângulos, basta multiplicar um lado pelo outro, porém, para calcular a área de outras figuras, devemos fazer a divisão em triângulos. Mas por que é diferente para quadrados e retângulos?

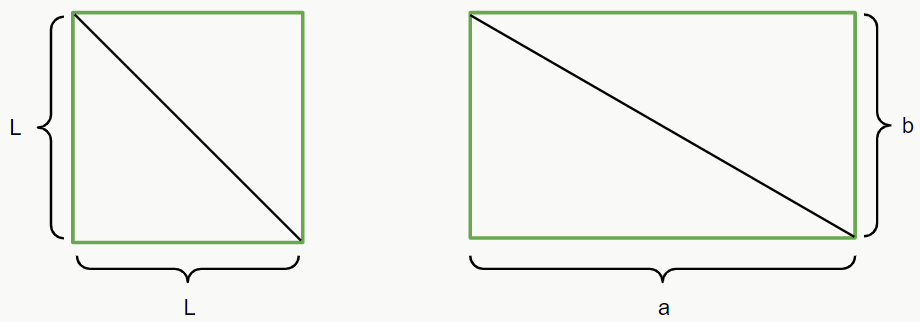
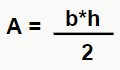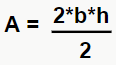Na verdade, não é. Perceba que ambas as figuras podem ser divididas em dois triângulos retângulos. Então para calcularmos a área delas, basta calcular a área desses triângulos. E qual a fórmula da área de um triângulo retângulo? Isso mesmo, área do triângulo , e como temos dois triângulos em cada figura, multiplicamos essa fórmula por 2, ou seja, área do triângulo vezes 2 .

No entanto, ao fazer isso, podemos cancelar os 2 do numerador e do denominador, correto? Dessa forma, temos que a área será simplesmente o produto base (b) pela altura (h), ou seja, A= b*h. E no caso das nossas figuras, a base e a altura são justamente os seus lados. 🙂

Vamos fazer o mesmo procedimento para outras figuras. Entendendo esse processo você conseguirá descobrir a área de qualquer polígono regular.

Ex. 1: área do losango

A figura acima é um losango. Perceba que, adicionando a diagonal maior (D) e a diagonal menor (d), ele pode ser dividido em 4 triângulos retângulos que terão base = \( \frac{D}{2}\) e altura = \( \frac{d}{2}\). Então, para descobrir a área da figura, basta descobrir as áreas dos quatro triângulos. Como eles são todos iguais, temos a seguinte expressão:

\[ A = \frac{4*\frac{D}{2}*\frac{d}{2}}{2} = \frac{4*D*d}{8} \] \[ A = \frac{D*d}{2} \]

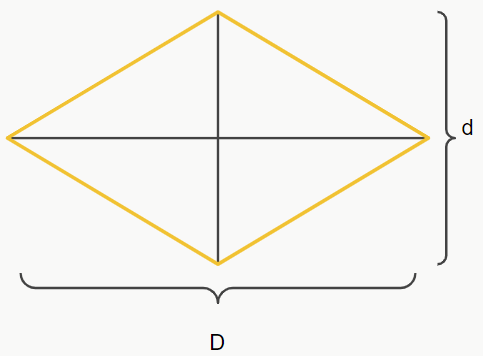
Portanto, a área do losango pode ser calculada a partir do produto das diagonais dividido por 2.

Ex. 2: área do hexágono

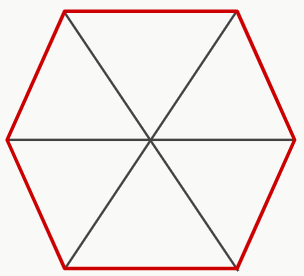
Perceba que o hexágono pode ser dividido em 6 triângulos equiláteros. Desse modo, se descobrirmos a área desses triângulos, iremos encontrar a área do hexágono. Na página sobre triângulos, aprendemos como calcular a área do triângulo equilátero. Sendo assim, podemos calcular a área do hexágono a partir da seguinte expressão:

\[ A = \frac{6*L^{2}*\sqrt{3}}{4} = \frac{3*L^{2}*\sqrt{3}}{2} \]

Portanto, é assim que se calcula a área de um hexágono regular.

Mas para que serve saber calcular tudo isso? O cálculo de área e perímetro é muito importante para diversas situações, vamos dar uma olhada em algumas delas.

Aplicações

1) Para saber a quantidade de material necessário para cercar uma área, devemos saber qual o perímetro dessa área.

2) Para se ter um melhor entendimento sobre a evolução do desmatamento, mede-se a área desmatada para que haja comparação com outros períodos de mesmo intervalo de tempo.

área desmatada da Floresta Amazônica — Imagem aérea do desmatamento na Floresta Amazônica, em 22 de setembro de 2017 – CARL DE SOUZA / AFP

Estes são apenas alguns poucos exemplos do uso de perímetros e áreas, mas existem muitos outros. Consegue pensar em mais alguns?

<– Nomenclatura

Referências

Área e perímetro de polígonos

https://brasilescola.uol.com.br/matematica/poligonos.htm

https://www.todamateria.com.br/poligonos/

https://mundoeducacao.uol.com.br/matematica/poligonos.htm