Corpos redondos
Corpos redondos são sólidos geométricos que têm uma coisa em comum: a presença de figuras circulares em suas estruturas. Além disso, esses sólidos, diferentemente dos poliedros, não apresentam faces laterais. Outro nome dado a eles é sólidos de revolução.
Cone
O cone é um corpo redondo formado por uma base circular e por uma superfície lateral curva, que é constituída por um triângulo que foi girado em torno do ponto central da base.
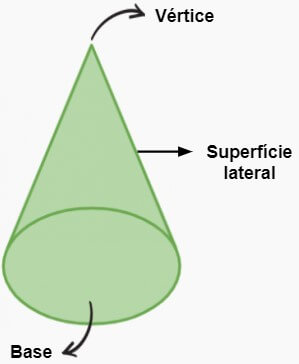
Área do cone
Ao planificar um cone, iremos nos deparar com a seguinte figura:
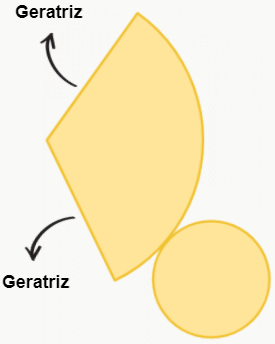
Os lados do “triângulo” que formam a superfície lateral do cone, como mostrado na figura, são chamados de geratriz, e suas medidas serão necessárias para calcularmos a área total do cone.
Mas como calcular a geratriz? Para isso teremos que utilizar o Teorema de Pitágoras da seguinte maneira:
g2 = r2 + h2
Onde g é a geratriz, r é o raio da base e h é a altura do cone.
Sabendo o valor de g, podemos encontrar a área lateral:
Al = π*r*g
Feito isso, precisamos da área da base:
Ab = π*r2
Por fim, é só juntar tudo e somar:
A = Ab + Al
ou
A = r * π(r + g)
Vamos ver um exemplo:
Exemplo: encontre a área de um cone de raio 4 cm e altura 7 cm.
Para calcular a área do cone, precisamos saber a medida da geratriz. Como sabemos a altura e o raio, podemos usar o Teorema de Pitágoras para encontrar a geratriz, certo? Desse modo:
Agora é só substituir na fórmula da área:
Volume do cone
Calcular o volume é mais simples, pois precisamos apenas saber o raio da base e a altura. Sabendo de ambas informações, basta utilizar a fórmula:
Ex. 1: calcule o volume de um cone de raio 3 cm e altura 10 cm.
É uma mera aplicação de fórmula, né?
V = 94,2 cm3
Ex. 2: calcule o volume de um cone de raio 5 cm e geratriz de 8 cm
Hmm, precisamos da altura… Vamos usar o Teorema de Pitágoras então.
Agora é só aplicar a fórmula:
Que tal vermos onde encontrar essa figura para finalizarmos?
E vamos para a última figura do módulo, a esfera.


