Determinantes

O que é o determinante de uma matriz? Na verdade, a definição é bem complexa e é muito provável que você não irá encontrá-la tão cedo… Por enquanto, vamos dizer que um determinante é um número que está associado a uma matriz, porém, apenas matrizes quadradas (que têm o mesmo número de linhas e colunas). Espera, está perdido(a) nesse assunto de matrizes? Dê uma lida na página sobre esse conteúdo e volte aqui depois, é rapidinho e vai te ajudar bastante!

Para representar um determinante de uma matriz qualquer, por exemplo a matriz M, utilizamos a notação detM. As aplicações deste tópico se resumem a cálculos matemáticos, porém não deixam de ser menos importantes, pois são utilizados para encontrar soluções de sistemas lineares, calcular a área de triângulos a partir de suas coordenadas no plano cartesiano, descobrir se vetores possuem ou não dependência linear… Ou seja, é um conteúdo muito importante para a matemática, e como podemos ver, está ligado a várias outras áreas da disciplina. Mas como se calcula um determinante?

Determinante de matrizes de ordem 3 (Regra de Sarrus)

Até agora tudo tranquilo, né? Não se preocupe, vai continuar, porém agora teremos um pouco mais de trabalho, mas nada que um pouco de prática não deixe o processo bem simples. Uma matriz de ordem 3 é aquela que possui três linhas e três colunas, ou seja, nove elementos. Para calcular o determinante, temos que utilizar uma técnica especial, conhecida como Regra de Sarrus.

Essa regra consiste em seguir alguns passos. E para verificar esses passos, vamos utilizar a seguinte matriz como exemplo:

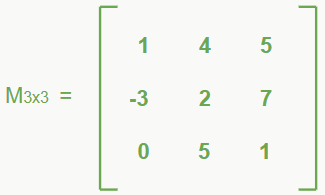
1- Pegamos as duas primeiras colunas da matriz e repetimos ao lado da terceira.

2- Multiplicamos os elementos das diagonais que possuem três elementos (primeiro no sentido da diagonal principal) para chegar na expressão:

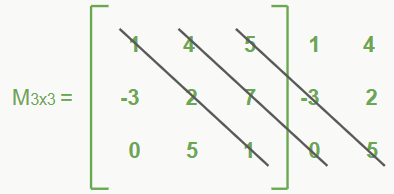
1*2*1 + 4*7*0 + 5*(-3)*5 = 2 + 0 -75 = -73

3- Multiplicamos os elementos das diagonais que possuem três elementos (agora no sentido da diagonal secundária) para formar o mesmo tipo de expressão, porém agora com sinal negativo ( – ).

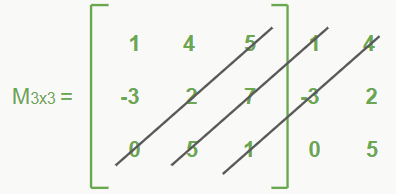
– (4*-3*1) – (1*7*5) – (5*2*0) = 12 – 35 – 0 = -23

4- Agora é só somar os dois valores encontrados:

-73 + (-23) = -96

Portanto, -96 é o determinante da nossa matriz 3×3.

Outra forma de encontrar o determinante

Existe ainda um outro jeito de encontrar o determinante de uma matriz 3 x 3, que é um pouco menos trabalhoso. Vamos utilizar a mesma matriz do exemplo anterior para ver se conseguimos o mesmo resultado:

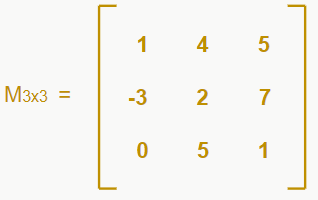
Na Regra de Sarrus, repetimos as duas primeiras colunas ao lado da terceira, porém, nesse caso não precisamos fazer isso. O que faremos neste método é retirar uma linha e uma coluna, formar matrizes 2×2, encontrar o determinante dessa matriz e multiplicar por um coeficiente (que será o número correspondente ao ponto de intersecção entre a linha e a coluna). Mas como escolhemos qual linha/coluna retirar?

Basta pegar os elementos da primeira linha, retirar a linha e a coluna das quais eles pertencem, e formar matrizes 2×2 a partir disso. Desse modo, temos na primeira linha 1, 4 e 5. Se retirarmos a linha e a coluna que o número 1 pertence, ficamos com a matriz 2×2:

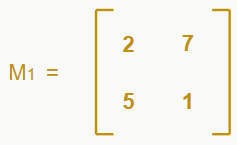
Calculando o determinante dessa matriz, chegaremos a detM1 = -33. Mas ainda temos que multiplicar pelo coeficiente, que é… exatamente, 1, pois é ponto em comum entre a linha e a coluna que retiramos. Fazendo isso, temos que 1*-33 = -33.

Agora repetimos o mesmo procedimento para os outros elementos da linha. Retirando a linha e coluna do 4, temos a matriz 2×2:

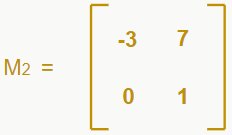
Calculando o determinante e multiplicando por 4, temos que -3*4 = -12. Retirando a linha e coluna do 5, temos a matriz 2×2:

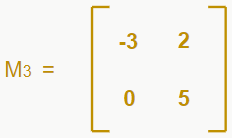
Calculando o determinante e multiplicando por 5, temos que -15*5 = -75. Com os três determinantes em mãos, iremos aplicar uma fórmula bem bacana:

detM1 – detM2 + detM3 = detM

Substituindo na fórmula: -33 – (-12) + (-75) = -33 + 12 + (-75) = -96. Exatamente o mesmo valor encontrado anteriormente. Lembrando que M, M1, M2 e M3 são apenas notações que escolhemos para esse exemplo, não precisa se apegar a elas, o importante é saber que a fórmula utiliza os valores sempre da esquerda para a direita.

Se preferir, pode fazer tudo junto ao invés de calcular cada determinante separadamente e depois juntar. Nesse caso, ficaríamos com a expressão:

1*(2*1-7*5) – 4*(-3*1) + 5*(-3*5) = -33 +12 – 75 = -96

Entendeu? detM1 = 1*(2*1-7*5), detM2 = 4*(-3*1)  e detM3 = 5*(-3*5).

Antes de avançarmos, gostaria de te mostrar algumas propriedades que serão muito úteis.

Dicas para facilitar a vida (no cálculo de determinantes)

1) Em uma matriz, se uma das linhas ou colunas tiver todos os seus elementos iguais a zero, o determinante será automaticamente 0.

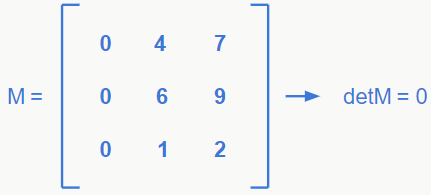
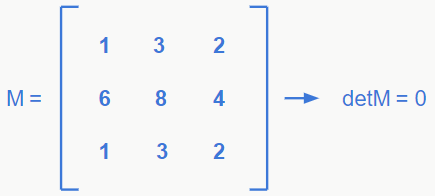
2) Se duas linhas ou duas colunas de uma matriz forem exatamente iguais, então o determinante dessa matriz é 0.

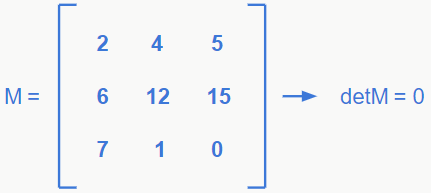
3) Se em uma matriz, duas linhas ou colunas tiverem elementos com valores proporcionais (um é o dobro do outro, o triplo, metade, …), então o determinante da matriz é 0. Note que no exemplo a seguir, os elementos da segunda linha são o triplo da primeira.

Por fim, vamos ver algo mais complexo: o Teorema de Laplace e as matrizes de ordem 4.

Referências