Determinantes
O que é o determinante de uma matriz? Na verdade, a definição é bem complexa e é muito provável que você não irá encontrá-la tão cedo… Por enquanto, vamos dizer que um determinante é um número que está associado a uma matriz, porém, apenas matrizes quadradas (que têm o mesmo número de linhas e colunas). Espera, está perdido(a) nesse assunto de matrizes? Dê uma lida na página sobre esse conteúdo e volte aqui depois, é rapidinho e vai te ajudar bastante!
Para representar um determinante de uma matriz qualquer, por exemplo a matriz M, utilizamos a notação detM. As aplicações deste tópico se resumem a cálculos matemáticos, porém não deixam de ser menos importantes, pois são utilizados para encontrar soluções de sistemas lineares, calcular a área de triângulos a partir de suas coordenadas no plano cartesiano, descobrir se vetores possuem ou não dependência linear… Ou seja, é um conteúdo muito importante para a matemática, e como podemos ver, está ligado a várias outras áreas da disciplina. Mas como se calcula um determinante?
Selecione aqui o conteúdo que deseja ver!
Determinante de matriz de ordem 4 (Teorema de Laplace)
A partir deste determinante as coisas começam a ficar mais complicadas, então este será o último que iremos aprender. Para calculá-lo, utilizamos o chamado Teorema de Laplace.
Mas o que diz esse Teorema?
O Teorema nos fornece um método para encontrarmos o determinante de matrizes quadradas de ordem 4 ou superior. Para isso, temos que seguir alguns passos:
1- Selecionamos uma linha ou coluna da matriz, que pode ser qualquer uma de sua preferência. Mas fica a dica, quanto mais zeros na linha, mais fácil é o cálculo do determinante.
2- Multiplicamos os elementos da fila pelos seus respectivos cofatores, e depois somamos todos os valores encontrados.
Calma aí, o que é esse tal de “cofator”?
Cofator
O cofator nada mais é que um número que representa um dado elemento da matriz. Para calculá-lo, utilizamos a seguinte fórmula:
Aij = (-1)(i+j) * detij
Onde:
- Aij = cofator do elemento que ocupa a posição “i” e “j”.
- i = linha ocupada pelo elemento.
- j = coluna ocupada pelo elemento.
- Detij = determinante da matriz formada pela retirada da linha “i” e coluna “j”.
Exemplo: vamos determinar o cofator do elemento a11 da matriz 3×3 a seguir.
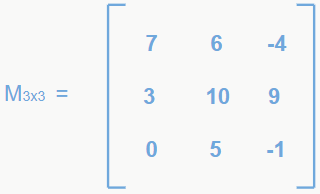
Como queremos saber o cofator do elemento a11, temos que eliminar a linha e a coluna das quais ele pertence.
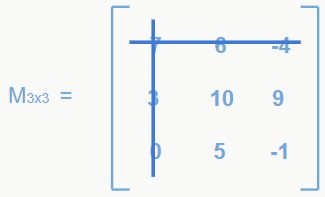
Feito isso, basta calcular o determinante da matriz 2×2 formada após a retirada da linha e coluna do elemento a11 e aplicar a fórmula do cofator.
10*(-1) – (9*5) = -10 – 45 = -55
Aplicando a fórmula:
A11 = (-1)(1+1) * (-55)
A11 = 55
Tranquilo, né?
Teorema de Laplace
Para entendermos melhor como funciona o Teorema, nada melhor que a prática, então vamos direto para um exemplo, assim vai ficar bem mais fácil de compreender o que devemos fazer.

Como não temos nenhuma linha/coluna com 0, vamos escolher qualquer uma, por exemplo, a linha 2, composta por 1, 3, 7 e 4. Para encontrar o determinante, precisamos multiplicar os elementos da linha/coluna pelos seus respectivos cofatores, e depois somar todos os valores encontrados. Desse modo, teremos que:
detM = 1*A21 + 3*A22 + 7*A23 + 4*A24
Calculando os cofatores:
A21 = (-1)(2+1) * detM1

A21 = (-1)(2+1) * (-298) = 298
A22 = (-1)(2+2) * detM2

A22 = (-1)(2+2) * (-134) = -134
A23 = (-1)(2+3) * detM3

A23 = (-1)(2+3) * (176) = -176
A24 = (-1)(2+4) * detM4
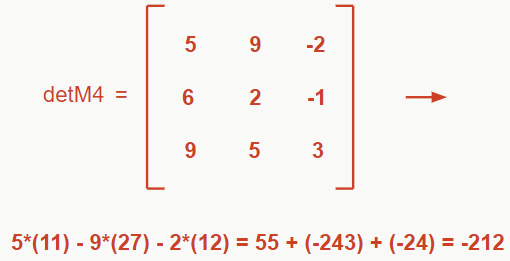
A24 = (-1)(2+4) * (-298) = -212
Retomando a fórmula inicial:
detM = 1*A21 + 3*A22 + 7*A23 + 4*A24
detM = 1*298 + 3*(-134) + 7*(-176) + 4*(-212)
detM = 298 – 402 – 1232 – 848
detM = -2184
Ufa, finalmente acabamos, deu um pouco de trabalho, mas não é tão difícil, é só tomar cuidado para não se perder no meio de tantos cálculos.
E terminamos aqui o conteúdo sobre determinantes. Apesar de ser bem trabalhoso, não é nenhum bicho de sete cabeças, e com a prática todos esses processos ficam tranquilos de serem feitos!