Matrizes
Matriz não é lá um nome que ouvimos com frequência, mas este elemento é muito importante para a matemática e tenho certeza de que você já deve ter visto em algum lugar, mesmo sem saber. Basicamente, uma matriz é uma tabela, composta de linha e colunas, que é utilizada para relacionar números.
Selecione aqui o conteúdo que deseja ver!
Operações com matrizes
Existem quatro tipos de operações que podem ser feitas entre matrizes, sendo elas: adição, subtração, multiplicação e multiplicação por número real. Vamos ver agora como executar cada uma delas.
– Adição
Para que seja possível somar duas matrizes, é necessário primeiro que elas sejam do mesmo tipo, ou seja, que tenham o mesmo número de linhas e colunas. A adição é feita a partir da soma dos elementos que ocupam as mesmas posições. Exemplo:
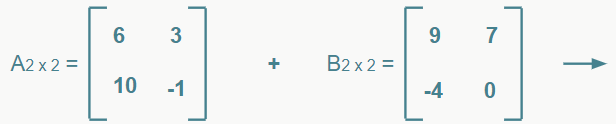
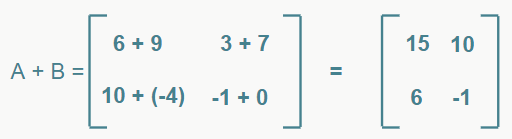
– Subtração
Da mesma forma que a adição, na subtração basta subtrair os elementos que estão na mesma posição. Mas cuidado, a ordem em que você executa a operação irá mudar o sinal dos seus resultados, ou seja, sendo duas matrizes A e B, A – B é diferente de B – A. Exemplo:
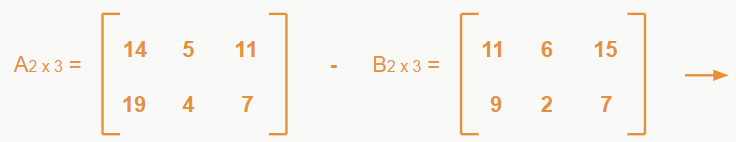

– Multiplicação
Até agora, vimos que as operações de adição e subtração não tem diferença alguma em relação àquilo que já estamos acostumados a fazer em qualquer conta comum. Porém, com a multiplicação é diferente.
Primeiro, para que seja possível realizarmos essa operação, temos que observar se o número de linhas da primeira matriz é igual ao número de colunas da segunda, pois esses valores serão a quantidade de linhas e colunas da matriz gerada pela multiplicação. Se isso acontecer, ótimo, podemos multiplicá-las, porém, se essa condição não for atendida, aí não podemos fazer essa operação.
Hmm, então se for verificado que o número de colunas de uma matriz é igual ao número de linhas da outra, basta então fazer a multiplicação normal, certo? Não, a regra aqui é um pouco diferente.
Em uma multiplicação de matrizes, devemos multiplicar os elementos da linha da primeira matriz pelos elementos da coluna da segunda matriz e somar esses produtos. Por exemplo, se tivermos duas matrizes A3x2 e B2x3, multiplicamos o 1° elemento da linha 1 da matriz A pelo 1° elemento da coluna 1 da matriz B, somamos ao produto do 2° elemento da linha 1 da matriz A pelo 2° elemento da coluna 1 da matriz B e assim por diante.
Lendo pode parecer um pouco confuso e complicado, mas não é tanto assim, vamos ver um exemplo para deixar tudo mais fácil:
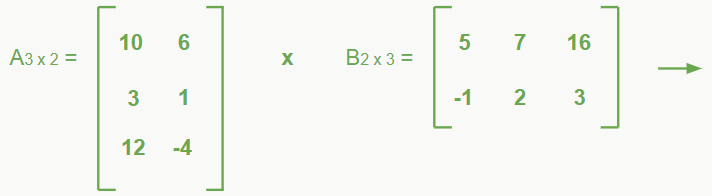
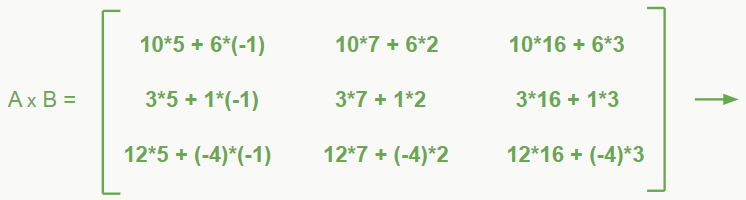
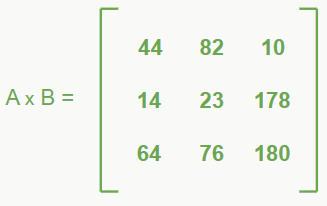
– Multiplicação por número real
Multiplicar uma matriz por um número real qualquer é bem simples, basta pegar esse número e multiplicar por todos os elementos da matriz, gerando assim, uma nova matriz. Exemplo:
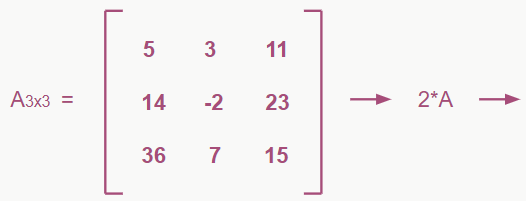
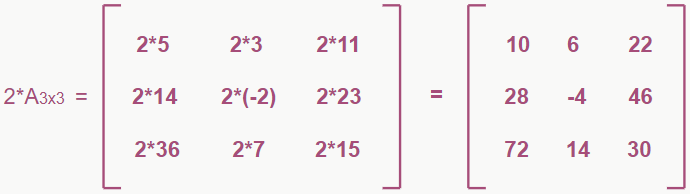
E chegamos ao fim das coisas que envolvem teoria nesse assunto. Mas calma aí, ainda falta ver as aplicações!