Sistemas Lineares
Sistemas lineares são conjuntos de equações associadas entre si e que possuem duas ou mais variáveis. Em sistemas lineares, entram apenas equações lineares, ou seja, expressões onde o maior expoente das incógnitas é igual a 1.
Selecione aqui o conteúdo que deseja ver!
Método de solução: Regra de Cramer
A Regra de Cramer é outro método de solução de sistemas lineares. Nele, iremos utilizar determinantes para encontrar nossas soluções. Lembre-se do que são o determinante principal e os determinantes secundários, pois é a partir deles que encontraremos nossas soluções. Desse modo, devemos calcular o determinante principal, os determinantes secundários para cada uma das variáveis presentes no sistema, e utilizar a seguinte fórmula:
Onde n é uma variável qualquer (que queremos encontrar o valor), Dn é o determinante secundário e D é o determinante principal. É importante ressaltar que essa fórmula deve ser utilizada para cada uma das variáveis presentes no sistema, ou seja, em um sistema com três variáveis, teríamos que encontrar o determinante secundário de todas e aplicar a fórmula para cada uma delas, a fim de encontrar seus respectivos valores. Vamos fazer um exemplo para entender melhor como funciona a Regra de Cramer?
Exemplo: vamos utilizar o mesmo sistema de três equações da página anterior, para você ver como esse método é muito mais simples e resulta em valores que também satisfazem a equação.
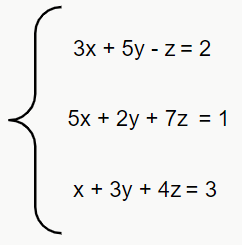
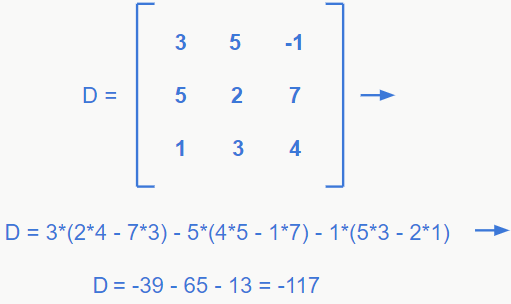
Para começar, vamos encontrar o determinante principal do sistema.
Feito isso, devemos encontrar os determinantes secundários para aplicar a fórmula:
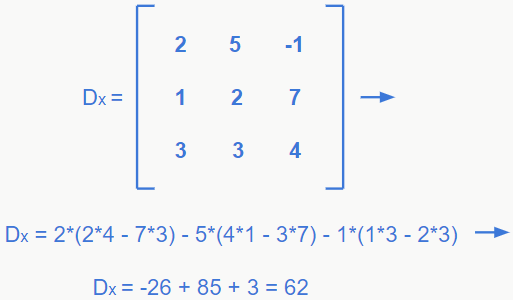
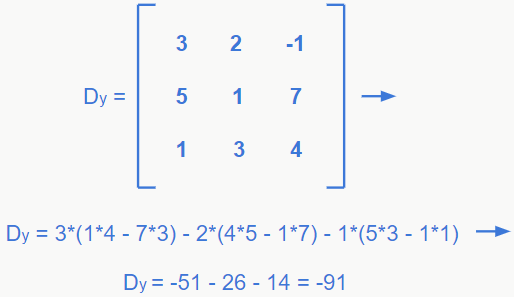
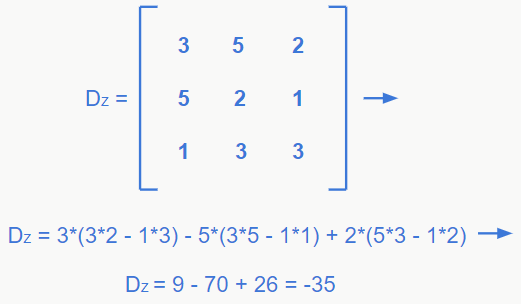
Por fim, é só aplicar a fórmula para encontrar x = -62/117, y = 91/117 e z = 35/117.
Viu como é fácil? Os resultados encontrados foram diferentes para os dois métodos utilizados, e isso é normal, não precisa se preocupar, o importante é que todos eles são pontos que satisfazem as equações do sistema.