Matrizes
Matriz não é lá um nome que ouvimos com frequência, mas este elemento é muito importante para a matemática e tenho certeza de que você já deve ter visto em algum lugar, mesmo sem saber. Basicamente, uma matriz é uma tabela, composta de linha e colunas, que é utilizada para relacionar números.
Selecione aqui o conteúdo que deseja ver!
Tipos de matrizes
Existem vários tipos de matrizes, e o nome recebido dependerá da quantidade de linhas e colunas que as compõem, ou dos numerais presentes em determinadas posições.
– Matriz linha
É uma matriz formada apenas por uma única linha e várias colunas.

– Matriz coluna
É uma matriz formada por uma única coluna e várias linhas.

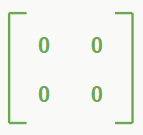
– Matriz nula
É uma matriz onde todos os seus elementos são iguais a 0.
– Matriz unitária
É uma matriz quadrada de ordem 1, ou seja, possui apenas 1 linha e 1 coluna.

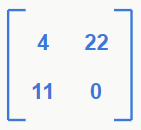
– Matriz quadrada
É uma matriz que possui o mesmo número de linhas e colunas. Nesse tipo de matriz, a quantidade de linhas e colunas é chamada de ordem da matriz.
Exemplos: Matriz de ordem 1 = M1 x 1, Matriz de ordem 2 = M2 x 2, Matriz de ordem 3 = M3 x 3, Matriz de ordem 4 = M4 x 4, …
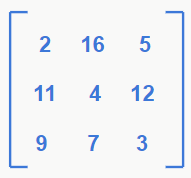

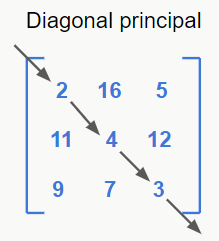
Nota-se também que esse tipo de matriz possui as chamadas diagonais primárias e secundárias, identificadas nas imagens a seguir.
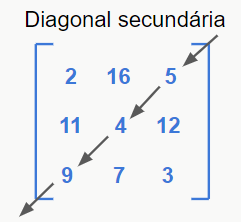
– Matriz diagonal
É uma matriz quadrada onde todos os elementos fora da diagonal principal são iguais a 0.
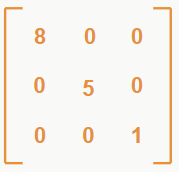
– Matriz identidade
É uma matriz quadrada onde todos os elementos da diagonal principal são iguais a 1 e todos os elementos fora dessa diagonal são iguais a 0.

– Matriz oposta
Dada uma matriz A, a matriz oposta pode ser obtida invertendo o sinal de todos os elementos da matriz original A. Na prática, estamos pegando a matriz original A e multiplicando por -1.
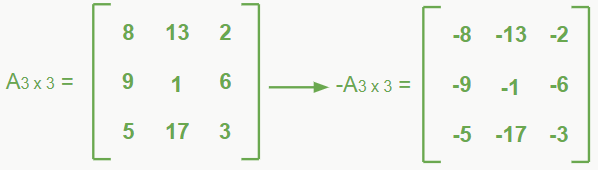
– Matriz igualdade ou igualdade de matrizes
São matrizes que possuem a mesma quantidade de linha/colunas e os mesmo elementos.
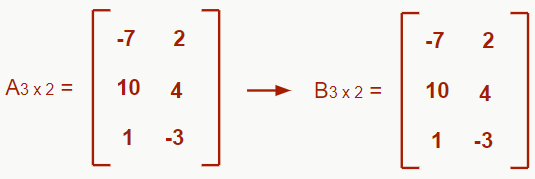
– Matriz transposta
É obtida a partir da troca ordenada de linhas por colunas (e vice-versa), ou seja, todos os elementos de uma linha passam a ser elementos de uma coluna, e todos os elementos de uma coluna passam a ser elementos de uma linha. Seja M a matriz original, a transposta é denotada por Mt.
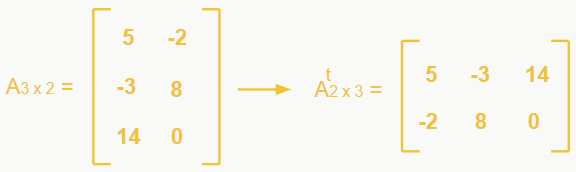
É isso aí, esses foram os tipos de matrizes. Na página seguinte iremos ver como realizar operações com matrizes.