Funções

Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação? 

Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.

Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂

Aplicações de funções

Vamos agora finalmente descobrir onde utilizar o conceito de funções e até mesmo algumas aplicações das próprias funções no cotidiano. O conceito de funções pode ser utilizado de várias formas, pois como sabemos, uma função é uma relação entre dois conjuntos, onde um conjunto (a imagem) depende do outro (o domínio) para acontecer. Por exemplo:

1) A numeração de um sapato é uma função do tamanho do pé, ou seja, para que um sapato tenha chance de ser comprado, é necessário que haja um pé com tamanho proporcional ao seu número.

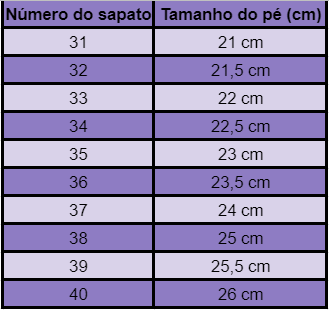
Neste primeiro exemplo, temos que o tamanho do pé é o domínio, e os números dos sapatos são a imagem do conjunto, pois afinal, a existência dos sapatos depende da existência dos pés, não é?

2) O tempo necessário para percorrer uma certa distância é uma função da velocidade, pois para cada velocidade média, há um tempo associado. Isso pode ser percebido, por exemplo, em provas de corrida no atletismo, onde cada corredor obtém um tempo diferente para o mesmo percurso.

Nesse segundo exemplo, o tempo necessário para completar uma prova de corrida depende da velocidade do atleta, e não o contrário. Desse modo, a velocidade é o domínio e o tempo é o nosso conjunto imagem. A figura a seguir apresenta os recordes mundiais da modalidade de 100 metros rasos (atletismo). Perceba que, mesmo correndo o mesmo percurso (100 metros), há uma pequena diferença de tempo entre eles. Logo o tempo está em função da velocidade do atleta.

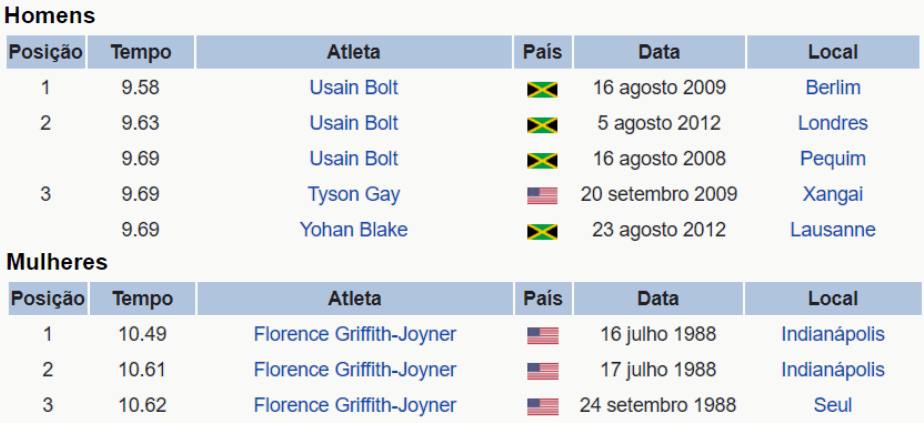
Estes são apenas alguns exemplos de como você pode utilizar o conceito de funções na sua vida, mas saiba que existem muitos mais. Pense aí, onde mais você poderia utilizar o conceito de funções? E faça mais, determine o domínio e a imagem da sua função, da mesma forma que fizemos aqui. Agora vamos ver alguns exemplos nos quais podemos construir funções.

3) O valor da gasolina é uma função da quantidade de litros abastecidos. Assumindo o valor da gasolina R$ 4,705, podemos criar uma função para representar esse valor.

f(x) = 4,705*x 

sendo x a quantidade de litros

4) Podemos também criar uma função que representa o salário de profissionais que recebem comissões, por exemplo. Supondo que o profissional receba um salário fixo de R$ 1200,00 e ganhe uma comissão de 5% sobre o valor todas de suas vendas, podemos criar a seguinte função:

f(x) = 0.05x + 1200

sendo x o valor total vendido pelo profissional

Mas por que eu faria isso no dia a dia? Bem, você pode criá-las para desenvolver uma planilha de gastos, prever diferentes cenários que podem ou não acontecer, acompanhar a evolução de algo ao longo do tempo através de um gráfico ou simplesmente para brincar de construir gráficos. 

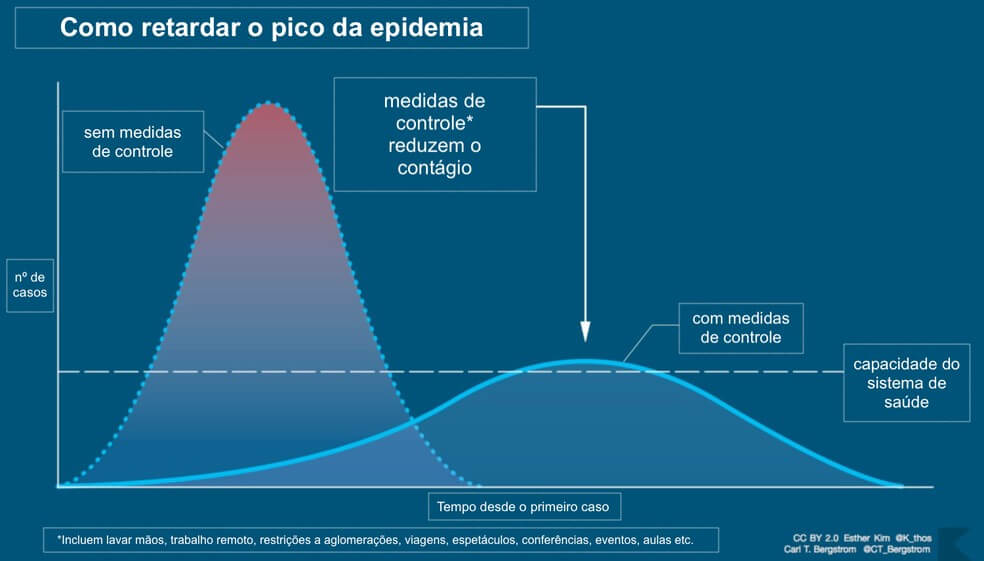
Um exemplo é um gráfico elaborado pelo cientista Drew Harris e adaptado pelo biólogo Carl Bergstrom, que mostra como medidas de controle podem ajudar no combate à pandemia da Covid-19.

O objetivo do gráfico é mostrar como medidas de contenção do vírus poderiam ajudar a evitar um colapso no sistema de saúde, implicando em um melhor atendimento dos que apresentarem sintomas não só da Covid-19, mas também de outras doenças.

Lembra que quando falamos sobre a função exponencial, foi dito que ele expressa bem o crescimento de bactérias e vírus? Olha só o que acontece com a expansão desse vírus sem nenhuma medida de controle… É isso mesmo, crescimento exponencial até chegar no pico, colapsando totalmente os serviços de saúde.

Eae, viu como podemos utilizar funções para várias coisas? É claro que algumas das funções apresentadas estão mais distantes de atividades cotidianas e você provavelmente não irá utilizá-las mesmo, mas muitos conceitos matemáticos podem ser aplicados em outros lugares além da matemática, como o conceito de funções, apresentado aqui, e o conceito de conjuntos, por exemplo. Além disso, conhecer funções e saber ler/interpretar gráficos corretamente é super importante para que você entenda bem a situação ou cenário que o gráfico quer representar, evitando, dessa forma, más interpretações de dados ou cenários. 🙂