Equações e Inequações
Equações e inequações são nomes bem parecidos, porém, isso não significa que tenham significados semelhantes.
Quando escrevemos uma equação, estamos criando uma igualdade, e por esse motivo, o sinal de igual ( = ) sempre deve aparecer em nossa expressão. Além disso, em uma equação, nosso objetivo é encontrar um ou mais números específicos que satisfaçam nossa expressão matemática. Portanto, em uma equação, uma coisa deve ser obrigatoriamente igual a outra, ou isso não será uma equação.
Já em uma inequação, estamos falando sobre uma desigualdade, e dessa forma, teremos os sinais de maior ( > ), menor ( < ), maior ou igual ( ≥ ) e menor ou igual ( ≤ ) em nossa expressão. O nosso objetivo agora não é encontrar um número específico, mas sim um conjunto de valores que satisfaçam nossa condição de desigualdade. As resoluções das inequações são praticamente iguais às das equações, exceto quando há mais de 1 resposta. Neste caso, você deverá avaliar quais das respostas fazem parte do conjunto solução, como veremos mais à frente.
Selecione aqui o conteúdo que deseja ver!
Equações do 1° grau
As equações e inequações de 1° grau são as formas mais simples de uma expressão matemática com incógnitas. Elas possuem esse nome pois o maior expoente encontrado nas expressões é 1. Dessa forma, vamos direto para a resolução de alguns exemplos:
Equação 1: 5x + 3 = 1
Como resolvemos isso?
Tanto em uma equação quanto em uma inequação, nosso objetivo será sempre achar o valor da incógnita (nesse caso, do “x”). Então, para alcançarmos nosso objetivo, temos que isolá-la, e para isso, temos que passar tudo que não for uma incógnita para o outro lado…
Passando para o outro lado…
Ué, cade a resolução? Calma, já vamos voltar para ela, mas antes disso, gostaria de te explicar o que realmente significa “passar para o outro lado da expressão”.
Você provavelmente já sabe que ao passar um número positivo para o outro lado ele fica negativo e vice-versa; e que ao passar um número que estava multiplicando, ele passa dividindo e vice-versa. Mas como isso acontece, é mágica? Claro que não, é matemágica! 😉
Vamos utilizar a mesma expressão de antes, aproveitando para resolvê-la: 5x + 3 = 1
Como foi dito, queremos isolar a incógnita, ou seja, deixá-la sozinha em um dos lados da expressão, e para que isso seja feito, precisamos eliminar todos os termos que não são uma incógnita. Como fazer isso?
Primeiramente, vamos lembrar de algo importante: sempre que você fizer alguma coisa de um lado da expressão, tem que fazer a mesma coisa do outro. Dessa forma, para eliminar o +3 do lado esquerdo, precisamos colocar um -3 do lado direito. Sendo assim, agora temos:
5x + 3 – 3 = 1 – 3
Somando o que pode ser somado, ficamos com:
5x = -2
Mas ainda falta tirar o 5, e para isso precisamos transformá-lo em 1, pois 1*x = x. Então basta dividir os dois lados por 5, não é? Fazendo isso, temos:
Entendeu? O que realmente acontece nessas passagens de um lado para o outro é que estamos, sem perceber, fazendo as operações necessárias para eliminar cada termo de um dos lados da expressão.
E essas “operações necessárias” serão sempre as operações inversas às presentes na expressão. Segue uma lista com as operações inversas:
- Adição e subtração;
- Multiplicação e divisão;
- Potenciação e radiciação (raízes);
- Logarítmo e exponencial.
Muito fácil, né? Vamos ver mais um exemplo para finalizar.
Equação 2: 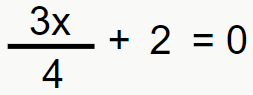
Neste exemplo, temos uma fração acompanhando o x, o que fazer então? A mesma coisa que fizemos no exemplo 1, isolar a variável! Primeiro começamos passando o 2 para o outro lado da equação:
Agora devemos passar o 4 multiplicando e o 3 dividindo (lembre-se das operações inversas). Fazendo isso, encontramos que:
E essas foram as equações de primeiro grau. Mas nada de parar por aqui, vamos ver algumas inequações!