Equações e Inequações
Equações e inequações são nomes bem parecidos, porém, isso não significa que tenham significados semelhantes.
Quando escrevemos uma equação, estamos criando uma igualdade, e por esse motivo, o sinal de igual ( = ) sempre deve aparecer em nossa expressão. Além disso, em uma equação, nosso objetivo é encontrar um ou mais números específicos que satisfaçam nossa expressão matemática. Portanto, em uma equação, uma coisa deve ser obrigatoriamente igual a outra, ou isso não será uma equação.
Já em uma inequação, estamos falando sobre uma desigualdade, e dessa forma, teremos os sinais de maior ( > ), menor ( < ), maior ou igual ( ≥ ) e menor ou igual ( ≤ ) em nossa expressão. O nosso objetivo agora não é encontrar um número específico, mas sim um conjunto de valores que satisfaçam nossa condição de desigualdade. As resoluções das inequações são praticamente iguais às das equações, exceto quando há mais de 1 resposta. Neste caso, você deverá avaliar quais das respostas fazem parte do conjunto solução, como veremos mais à frente.
Selecione aqui o conteúdo que deseja ver!
Equações logarítmicas
A equação logarítmica é aquela que possui ao menos um logaritmo na expressão. Mas antes de partirmos para as equações em si, vamos dar uma olhada em algumas informações importantes sobre os logaritmos.
Começando com restrições: para que exista um resultado para o logaritmo, ele deve ser maior que 0, ou seja, log(0) não existe; log(-3) não existe; log(11) existe. Portanto, fique muito atento a isso.
Agora falando sobre as bases do logaritmo: as mais utilizadas são a 2 e a 10. E como eu sei em qual base está meu logaritmo? Basta olhar para o “numerozinho” que acompanha o log, por exemplo, em log2(x), a base é 2; em log10(x), a base é 10.
Mas e quando não tem nenhum “numerozinho” escrito? Nesse caso, estamos falando de um log com base 10, então log10(x) = log(x). Há ainda um outro tipo de logaritmo bastante utilizado, que é conhecido por ln (ou logaritmo natural) e utiliza a base e (número irracional de Euler), que vale aproximadamente 2,72. O ln é o inverso da exponencial ex .
Por fim, antes de resolvermos algumas equações, devemos falar das propriedades dos logaritmos.
Propriedades dos logaritmos
1) O logaritmo da multiplicação de dois ou mais números é igual a soma dos logs desses números e vice-versa. Exemplo:
log(5*7) = log(5) + log(7)
2) O logaritmo da divisão de dois ou mais números é igual a subtração dos logs desses números e vice-versa. Exemplo:
log(8/3) = log(8) – log(3)
3) Se o valor dentro do log tem um expoente, este expoente passa a multiplicar o log e vice-versa. Exemplos:
log(x2) = 2 * log(x)
log(5x) = x * log(5)
Agora que já sabemos de todas as informações necessárias, vamos ver algumas equações.
Equação 1: log(2x + 10) = log(-x + 1)
Como os logaritmos possuem a mesma base, podemos cortá-los da equação. Desse modo, ficamos com:
2x + 10 = -x + 1
2x + x = -10 + 1
3x = -9
x = -3
Importante! Você só poderá realizar esse “corte” quando só houver Logs em ambos os lados. Se tiver uma adição, subtração, multiplicação ou divisão junto com os Logs, não é possível cortá-los.
Equação 2: log2(4 + 7x) = 5
Na equação 2, não podemos cortar o logaritmo, pois temos uma constante do outro lado da expressão. Mas para resolver é bem simples, basta pegar a base do log (2 nesse caso) e colocá-la como base do 5, que vai servir de expoente. Não entendeu? Vamos seguir com a resolução do exemplo que tudo irá ficar mais claro.
log2(4 + 7x) = 5
4 + 7x = 25
Entendeu agora? Quando você encontrar um logaritmo igualado a uma constante, basta pegar a base do Log e passar para o outro lado da equação para que ela se torne a base da constante.
4 + 7x = 25
4 + 7x = 32
7x = 32 – 4
7x = 28
x = 4
Equação 3: log10 (4x – 2) = log10 2 – log10 (2x – 1)
Na equação 3, apesar de termos todos os logs com a mesma base, não podemos cortá-los, pois há uma subtração do lado direito da equação. Então devemos usar as propriedades vistas anteriormente.
Primeiramente, temos que usar a propriedade 3 para transformar a subtração em divisão.
Agora perceba que podemos cancelar os Logs, pois não há mais nada atrapalhando.
Então basta resolver a equação normalmente.
Veja que podemos dividir a equação por 8, tornando-a mais simples de ser resolvida.
Se você calcular essa equação de 2° grau, encontrará x1 = 0 e x2 = 1. Mas não acabou por aí, lembre-se de que sempre temos que verificar se nossa equação possui alguma restrição, e como sabemos, um Log não pode ser menor ou igual a 0.
Sabendo disso, devemos testar as raízes encontradas.
Testando o 0, vemos que log10 (4*0 – 2) = log10 ( – 2), portanto, não precisamos nem continuar os testes, pois esse aí já não satisfaz a equação, já que é um Log de número negativo.
Testando o 1, vemos que log10 (4*1 – 2)= log10 ( 2), e log10 (2*1 – 1) = log10 (1), portanto, 1 satisfaz a equação e é nossa única resposta para a equação.
Equação 4: log(2x2 + 3x – 4) = 2 log (x)
Na equação 4, temos novamente que usar as propriedades, pois não podemos cancelar os Logs por conta da multiplicação entre 2 e log (x). Para resolver, basta utilizar a propriedade 3.
log(2x2 + 3x – 4) = log x2
Agora é só cancelar e resolver normalmente a equação quadrática.
2x2 + 3x – 4 = x2
x2 + 3x – 4 = 0
x1 = -4 e x2 = 1
Testando os valores na equação original, vemos que -4 não será solução, pois teríamos log (-4). Mas com o 1 não temos nenhum problema, pois log(2*12 + 3*1 – 4) = log(1) e log(x) = log(1). Portanto, 1 é nossa resposta final.
Equação 5: -4 * (log x)2 + 3 * log (x) = -1
Perceba que temos na expressão o termo (log x)2. Talvez ao olhar isso você tenha o instinto de querer utilizar a propriedade do expoente, porém note que o “quadrado” não é expoente do algarismo que está dentro do log, mas sim expoente do próprio Log (note que os parênteses estão separando os algarismos).
Desse modo, temos que fazer uma mudança de variável para resolver esta equação. Para isso, vamos dizer que log x = y e vamos fazer a substituição.
-4y2 + 3y = -1
-4y2 + 3y + 1 = 0
Agora já sabemos resolver de olhos fechados, não é mesmo?
Feitas todas as contas, você verá que y1 = -¼ e y2 = 1.
Acabou? Ainda não, pois perceba que encontramos os valores de y, mas a equação original tinha x, então temos que converter novamente os valores encontrados. Lembre-se que quando a base do logaritmo não é mostrada, é porque é base 10.
log x = -¼
x = 10(-¼)
x = 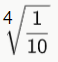
x = 0,56
log x = 1
x = 101
x = 10
Por fim, devemos testar os valores na equação original para ter certeza que não há nenhum log <= 0. Ao fazer isso, você verá que está tudo certo, portanto nossas respostas são 0,56 e 10.
Aplicação: a escala Richter
A escala Richter é uma escala utilizada para determinar a intensidade de terremotos. Foi desenvolvida pelo sismologista americano Charles F. Richter, em 1935.

Mas qual a relação entre ela e os logarítmos? A relação está no fato de que tanto a escala quanto a fórmula desenvolvida por Richter são baseadas em logarítmos.
Onde M = magnitude do terremoto, A = amplitude (em milímetros) do terremoto, Δt é o intervalo de tempo (em segundos) entre a onda superficial e a onda de pressão máxima do terremoto.
Mas como medimos A e Δt? Através de um aparelho chamado de sismógrafo. Na imagem a seguir, os “riscos” são lidos e analisados por especialistas, e a partir deles são retirados os valores de A e Δt, permitindo, dessa forma, o cálculo da intensidade do terremoto.

Mas nada de parar por aqui, vamos dar uma olhada nas equações exponenciais.
Referências
Propriedades dos logaritmos
https://www.todamateria.com.br/propriedades-dos-logaritmos/
Escala Richter
http://ecalculo.if.usp.br/funcoes/grandezas/exemplos/exemplo5.htm