Funções
Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação?
Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.
Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂
Selecione aqui o conteúdo que deseja ver!
Função exponencial
Na função exponencial, a incógnita encontra-se no expoente da expressão. No entanto, não é qualquer número que pode servir de base. Por exemplo, em bases negativas, a função não seria definida em valores como x = 1/2 (raiz quadrada), 1/4 (raiz quarta), 1/6 (raiz sexta), …, ou seja, em todas as raízes pares, pois como sabemos, não existem raízes reais para números negativos. Outra restrição dessa função em relação a base é que esta não pode ser 0 ou 1, pois afinal, 0 elevado a qualquer coisa é sempre 0, e 1 elevado a qualquer número é sempre 1.
Um outro aspecto sobre as bases das funções exponenciais é que elas definem se a função será crescente ou decrescente, mas relaxa que é bem tranquilo de verificar. Basicamente, se a base for maior que 1, a função será crescente; e se estiver entre 0 e 1, será decrescente.
Vamos ver alguns exemplos?
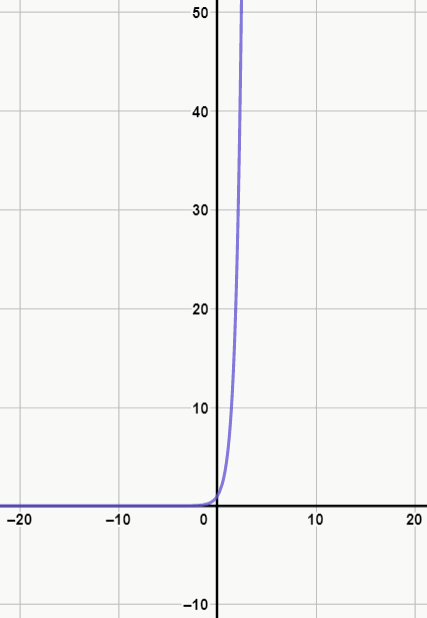
Ex. 1: 5x
Ex. 2: 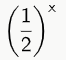
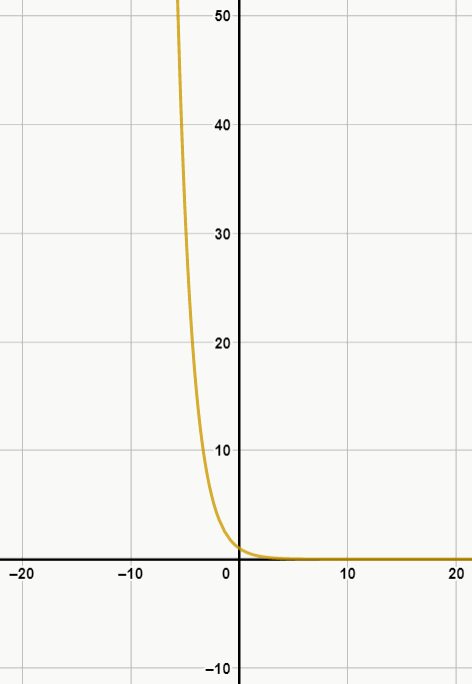
Perceba que, no exemplo 1, a função é crescente, enquanto no exemplo 2, a função é decrescente. Uma curiosidade sobre as funções exponenciais é que elas representam bem o crescimento de seres microscópicos, como bactérias e vírus, pois, caso não sejam tomadas ações para prevenir suas circulações, esses organismos se reproduzem muito rapidamente.