Funções
Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação?
Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.
Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂
Selecione aqui o conteúdo que deseja ver!
Função logarítmica
A função logarítmica é a inversa da exponencial e é caracterizada por possuir um logaritmo em sua estrutura. Essa função é definida como:
loga (x)
onde a é a base do logarítmo
Ela pode ser crescente ou decrescente, e isso dependerá da base do logaritmo. Se a base for maior que 1, a função é crescente, se for menor que 1, é decrescente. Dentre as bases maiores que 1, as mais utilizadas são a 2 e a 10, mas ainda há uma outra bem conhecida, que é a base e (chamado de número de Euler), que vale aproximadamente 2,71, e compõe o chamado logaritmo natural (denotado por “ln(x)”).
Um ponto importante sobre a função logarítmica é que ela não é definida para valores negativos de x, e isso acontece porque não há logs de número negativos no conjunto dos números reais. Perceba, nos exemplos a seguir, que a reta nunca passa para o lado negativo do eixo x.
Vamos ver como ficam os gráficos em cada uma dessas bases?
Ex. 1: log2(x)
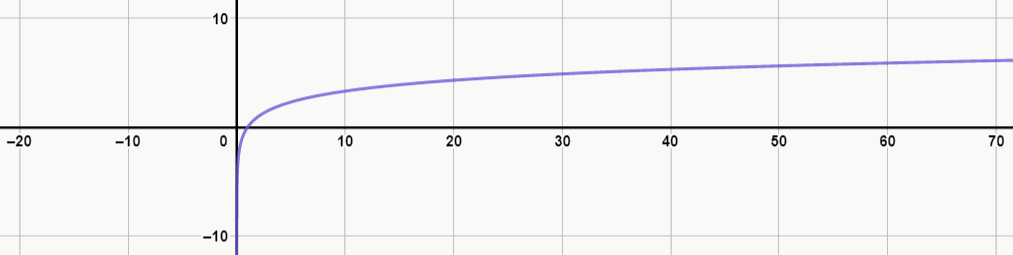
Ex. 2: log10(x)
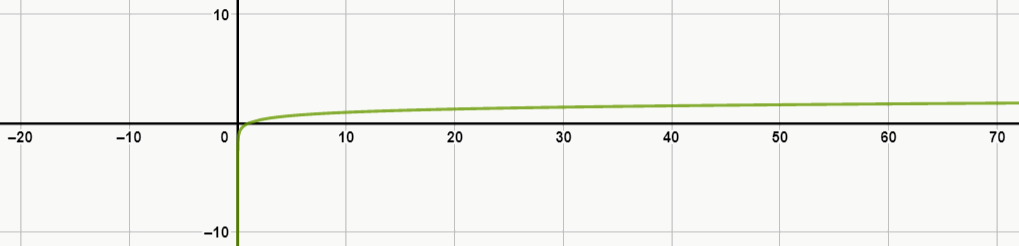
Ex. 3: ln(x)
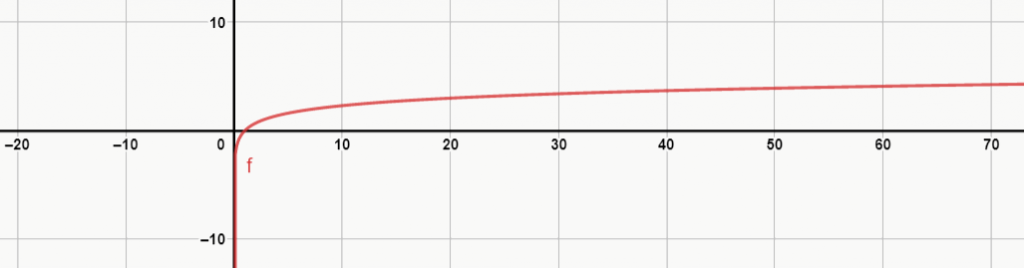
Ex. 4: log0,5(x)
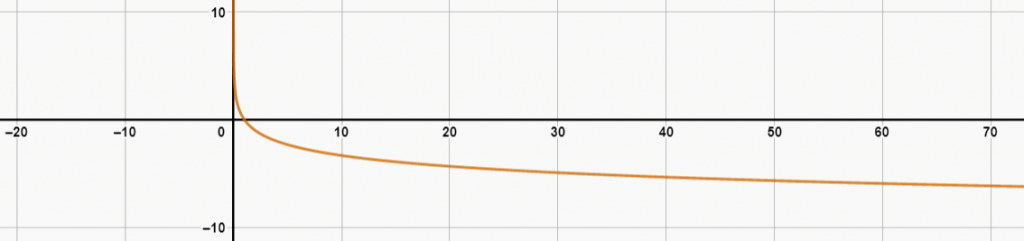
Note que, quanto maior é a base do logaritmo, mais lento é o crescimento do gráfico. Além disso, veja que, no exemplo 4, a função decresce, pois sua base é negativa.