Funções
Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação?
Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.
Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂
Selecione aqui o conteúdo que deseja ver!
Função modular
Uma função modular é aquela na qual todos os seus termos estão dentro de um módulo. Mas o que é um módulo?
O módulo de um número é, basicamente, sua parte positiva, ou seja, de um módulo só saem números positivos. Um valor em módulo é representado da seguinte forma: | x |, que quer dizer, o módulo de x.
Um outro modo de classificar o módulo de um número é dizer que ele representa a distância de um número até o zero, e como não existe distância negativa, o valor é sempre positivo.
Exemplos: | 4 | = 4; |-3| = 3.
E a função modular?
Em sua forma mais simples, a função modular é expressa da seguinte forma: f(x) = | x |
A seguir você pode visualizar seu gráfico. Perceba que, independente do número substituído na função, a resposta nunca é negativa, e por isso a reta nunca passa para o lado negativo do eixo y.
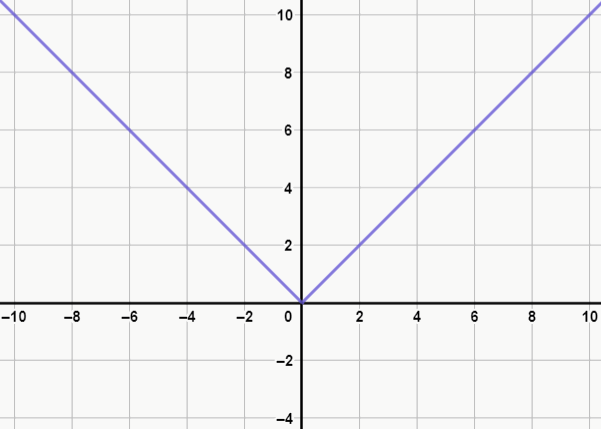
Só para fixar a ideia, vamos olhar mais uma função, agora um pouco mais complexa:
Ex. 1: f(x) = |x3 – x2 + 5|
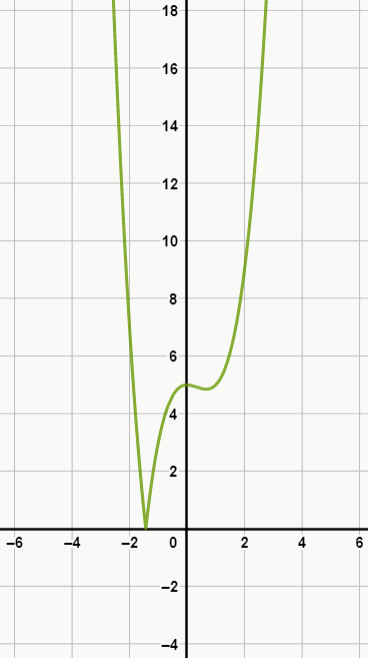
Olha aí, apesar da função ser esquisita, nada de reta na parte negativa do eixo y. Perceba que, ao chegar em y = 0, a função volta a subir. Vamos ver agora como seria o gráfico da mesma função, porém sem o módulo.
Ex. 2: f(x) = x3 – x2 + 5
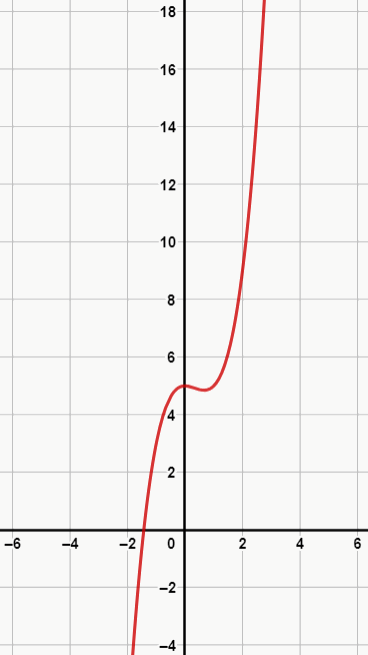
Viu como é diferente? Note que, nesse caso, em vez de subir na direção do eixo y, o gráfico desce na direção do lado negativo do eixo.