Funções
Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação?
Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.
Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂
Selecione aqui o conteúdo que deseja ver!
Função quadrática
Agora vamos elevar o nível do nosso expoente, pois a função quadrática, popularmente conhecida como “função de segundo grau” e formalmente por “função polinomial de segundo grau” possui 2 como maior expoente. E da mesma forma que a função afim, a quadrática também possui uma forma bem comum:
f(x) = ax2 + bx + c
onde a, b e c são números reais e a deve obrigatoriamente ser diferente de 0
Nesta forma, com todos os termos (a, b, c), é chamada de “função quadrática completa”.
Percebeu que foi dito que apenas a não pode ser 0? Isso ocorre pois, se a for igual a 0, o que nos sobra é uma função de primeiro grau, concorda? Isso também significa que b e c podem ser iguais a 0 e não aparecer na função, e quando isso acontece, damos a ela o nome de “função quadrática incompleta”.
E o gráfico da função quadrática, como é? No estudo sobre função afim, vimos que o gráfico era uma reta, porém, na função quadrática, a figura formada é uma parábola. Esta curva possui um elemento especial, que corresponde ao ponto onde a função muda de sentido (se estava crescendo passa a decrescer e vice-versa), que recebe o nome de vértice da parábola. Vamos ver alguns exemplos:
Ex. 1: 2x2 + x – 5 (a > 0)
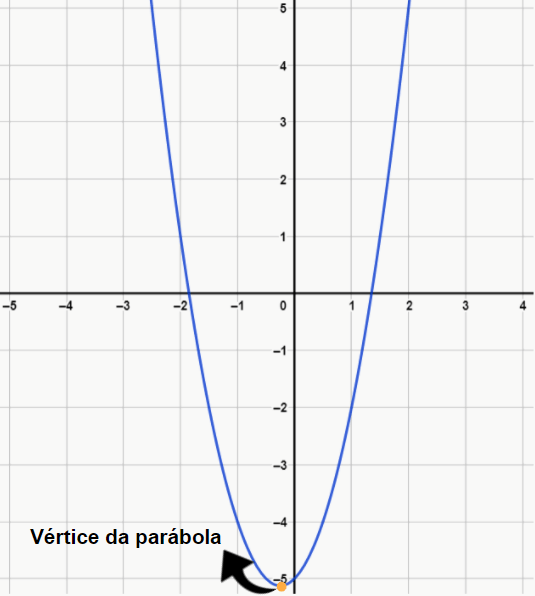
Ex. 2: -2x2 + x – 5 (a < 0)
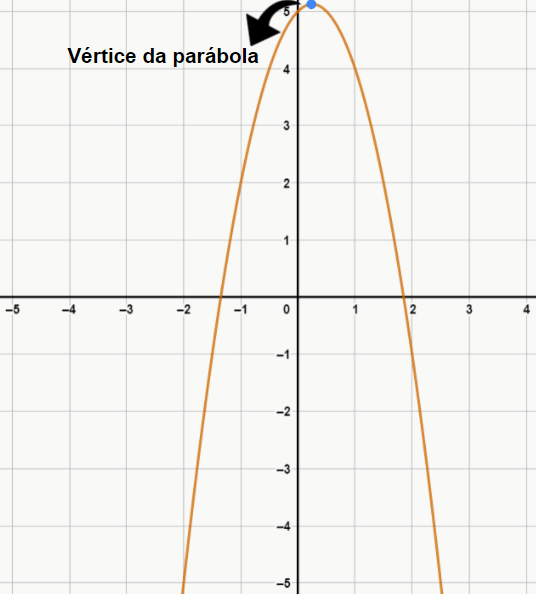
No exemplo 1, perceba que a concavidade (parte redondinha da figura) está virada para cima. Isso acontece pois o valor de a é positivo. Já no exemplo 2, veja que a concavidade está virada para baixo, e isso ocorre porque a é negativo. Quer uma dica para nunca esquecer essa relação entre o sinal de “a” e a concavidade? Pense assim, no exemplo 1, a concavidade está “olhando” na direção do lado positivo do eixo x, pois afinal, a é maior que 0. Enquanto isso, no exemplo 2, a concavidade está “olhando” na direção do lado negativo do eixo x, pois afinal, a é menor que 0.
Mas será que a função do termo a é só controlar a direção da parábola? E os outros termos, b e c, para que servem?
Os termos da função
- a: as funções do termo são: I) acompanhar o x2; II) definir a direção da parábola; e III) definir o achatamento da parábola. Quanto maior o valor de “a”, mais achatada é a parábola.
- b: a função do termo é definir a inclinação da parábola após passar do eixo y. De modo mais simples, pode-se dizer que ele define “a distância entre o vértice da parábola e o eixo y”. Se b < 0, a parábola decresce após passar pelo eixo; se b > 0, a parábola cresce após o eixo; se b = 0, não há inclinação na parábola. Quanto maior o valor de b, maior é essa inclinação (ou distância).
- c: a função do termo é definir o ponto em que a parábola cruza o eixo y. Se c < 0, a parábola corta o eixo y no lado negativo; se c > 0, a parábola corta o eixo y no lado negativo; se c = 0, a parábola corta o eixo y na origem.
Lendo pode parecer um pouco confuso, então vamos ver alguns gráficos para que possamos entender melhor a função de cada termo.
Ex. 3: f(x) = x2
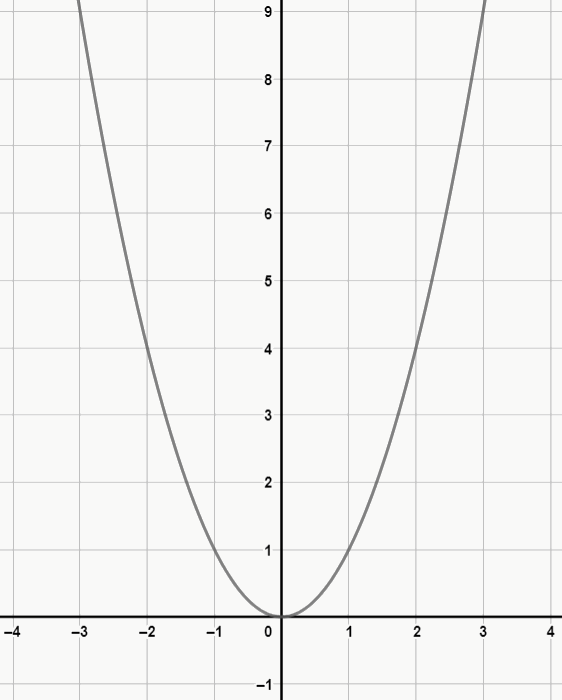
O exemplo 3 demonstra a parábola mais simples possível. Perceba que, como b e c são iguais a 0, o vértice da parábola passa pelo eixo y (ou seja, não possui inclinação) e encontra-se na origem.
Ex. 4: f(x) = 3x2 – 2
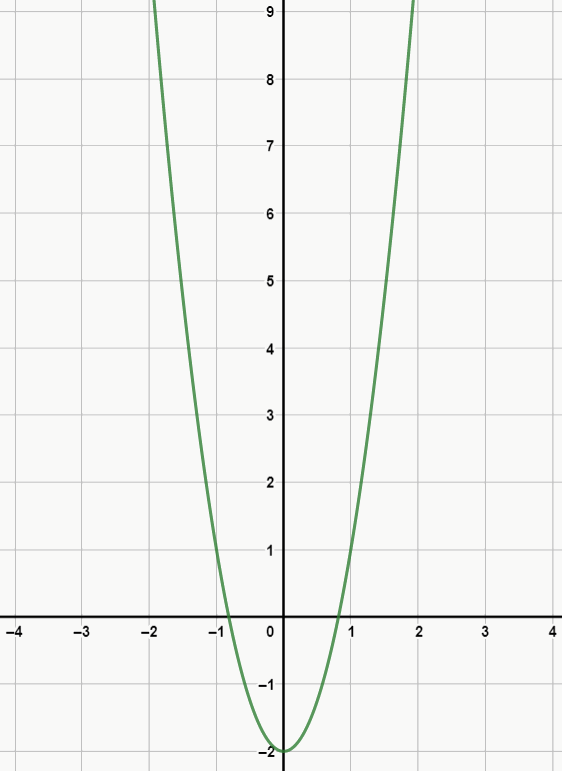
No exemplo 4, note que continuamos sem o b, portanto, nada de inclinação. Contudo, perceba que agora a parábola está mais achatada que no exemplo 3, e isso ocorre porque o valor de a é maior (3 ao invés de 1). Note também que o vértice da parábola está no ponto y = -2, e isso acontece pois temos c = -2.
Ex. 5: f(x) = x2 – 2x
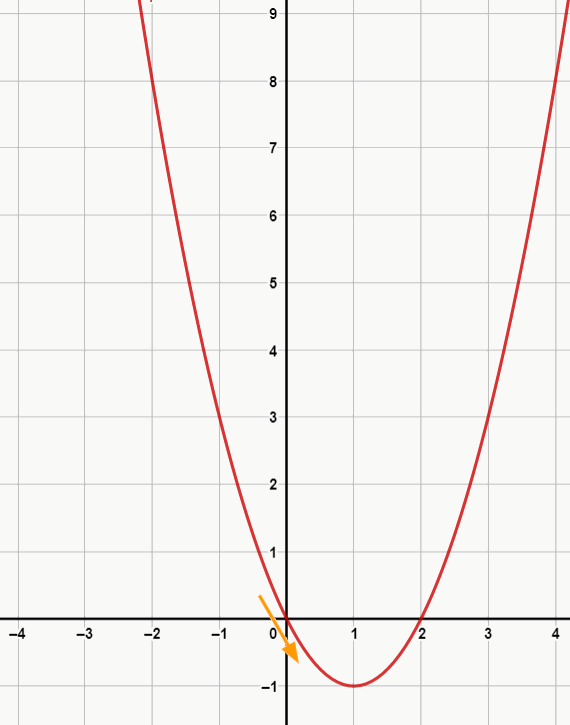
No exemplo 5, temos a = 1, e c = 0 (note que a curva passa pela justamente por y = 0), ou seja, nada novo. A novidade está no fato de que finalmente temos a aparição de b. Note que a parábola aparece deslocada na direção negativa do eixo y e decresce (veja a direção da seta) após passar pelo eixo, pois há agora a inclinação causada pelo b negativo.
Ex. 6: f(x) = x2 + x + 1
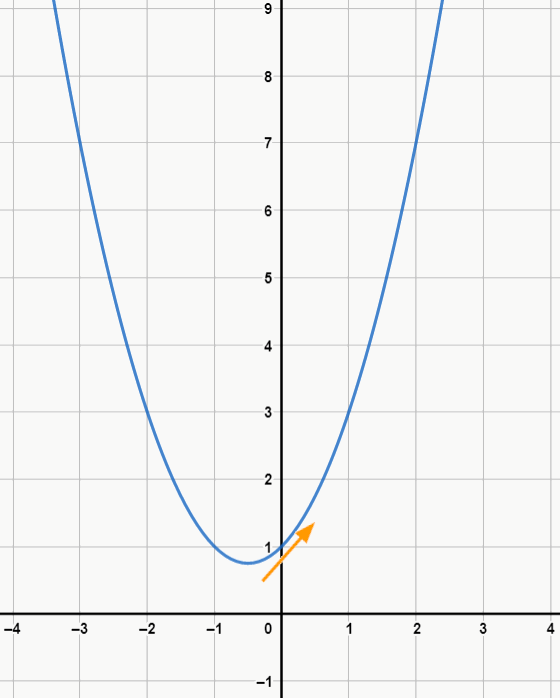
No exemplo 6 temos uma função quadrática completa. O interessante é que agora temos b e c juntos na expressão. Perceba que, como b é positivo, diferentemente do exemplo 5, a parábola aparece deslocada na direção positiva do eixo y e cresce (veja a direção da seta) após passar pelo eixo. Além disso, note que, como c = 1, a parábola corta o eixo em y = 1.
Ficou mais claro agora qual a função de cada um dos termos que compõem uma função quadrática? Agora você já está preparado(a) para construir várias parábolas por aí. 🙂
Aplicação: antenas parabólicas, espelhos e faróis
Você já deve ter ouvido falar de antenas parabólicas, mas sabe o que isso tem a ver com a função quadrática? A resposta está no próprio nome: antena parabólica, ou seja, antena em forma de parábola. Opa, olha que interessante, é a mesma curva que estudamos nesta página! Mas por que o formato de parábola? Isso ocorre por conta de uma propriedade das parábolas, que consiste na reflexão de ondas incidentes em sua superfície para um único ponto comum (chamado de ponto de foco). Desse modo, como as ondas de rádio são fracas, é necessário que haja uma grande superfície que receba esses sinais e os concentre em um ponto comum. Sendo assim, superfícies parabólicas são perfeitas para alcançar esse objetivo. Essa mesma propriedade é utilizada, por exemplo, nos faróis de automóveis (com ondas eletromagnéticas – luz), e em espelhos de telescópios.

Bem legal essa aplicação, né? 🙂 Mas, agora que já sabemos bastante sobre essa função, vamos partir para outro tipo então!
Referências
Função quadrática
https://www.educamaisbrasil.com.br/enem/matematica/funcao-quadratica
Aplicações da parábola