Funções
Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação?
Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.
Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂
Selecione aqui o conteúdo que deseja ver!
Funções constante
Uma função constante, como o próprio nome já diz, é uma função que tem sempre o mesmo resultado, não importando qual é o valor da variável. Vamos ver alguns exemplos para fixar o conceito.
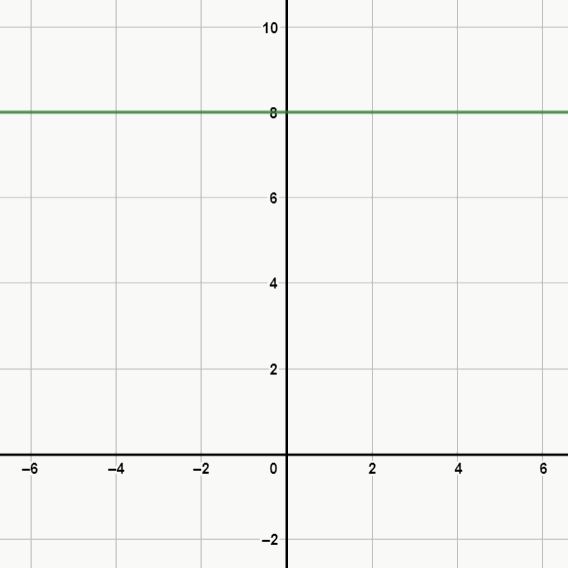
Ex. 1: f(x) = 8
Neste exemplo, a variável nem aparece na expressão, logo, o resultado será sempre o mesmo, 8. Veja como fica o gráfico deste exemplo:
Ex. 2: f(x) = 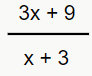
Ué, mas na página anterior foi dito que para uma função ser constante, a deve ser igual a zero, mas ali temos um 3x, será mesmo que essa função é constante?
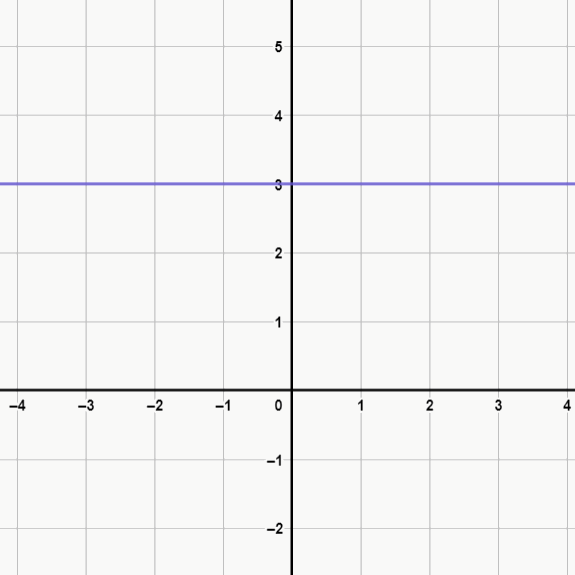
Neste exemplo, para concluirmos de fato que a função é constante, devemos fatorar a expressão do numerador (3x + 9). Feito isso, temos que 3*(x + 3), pois veja que, se você realizar esta operação, chegará novamente em (3x + 9). E opa, perceba que isso é exatamente igual ao que temos no denominador (x+3), portanto, podemos “cortá-los”, resultando em 3, ou seja, não há incógnita, então a = 0 e a função é mesmo constante. Veja como fica o gráfico deste exemplo:
Funções crescente e decrescente
Como dito na página anterior, quando a é um número positivo, a função é chamada de crescente, e quando a é um número negativo, é chamada de decrescente. Vamos ver alguns exemplos:
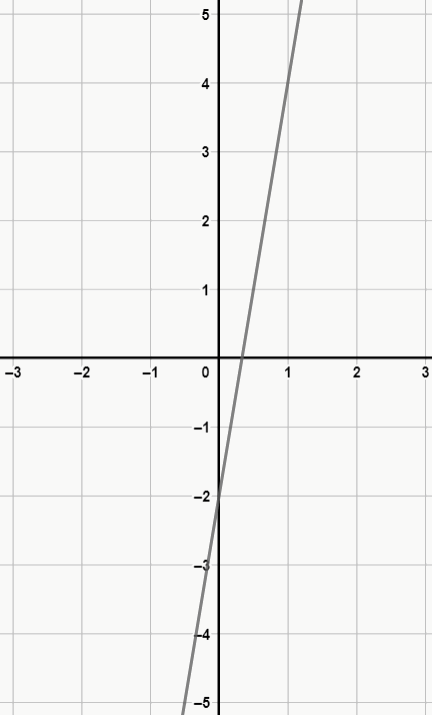
Ex. 1: f(x) = 6x – 2 (crescente: a > 0)
Ex. 2: f(x) = -6x – 2 (decrescente: a < 0)
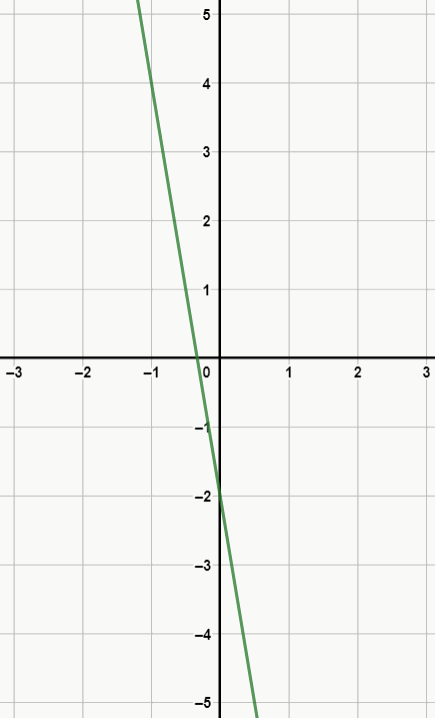
Observe que, apesar das funções serem semelhantes, o sinal faz toda a diferença no gráfico da função.
Muito interessantes esses casos particulares, né? Mas eles não acabam por aqui não, há mais alguns que são bem importantes! Vamos ver?
Referências
Casos particulares da função afim
https://www.infoescola.com/matematica/funcao-afim/
Função constante
https://mundoeducacao.uol.com.br/matematica/funcao-constante.htm