Funções
Antes de olhar para o conteúdo em si, gostaria de te perguntar: você sabe qual a diferença de uma função para uma equação?
Para começar, as duas diferem em definição, pois uma função, como veremos em breve, é uma relação entre dois conjuntos numéricos, enquanto uma equação é simplesmente uma expressão matemática que se iguala a outra. De um modo bem informal, você pode pensar que, em uma equação, nosso objetivo é encontrar um ou mais algarismos que satisfaçam a expressão; já quando pensamos em funções, queremos verificar o comportamento de uma expressão, normalmente através de um gráfico. Ou seja, equações geram números, enquanto funções geram retas/curvas.
Entendeu agora qual a diferença entre função e equação? Bem tranquilo, né? Ao longo das páginas você verá alguns gráficos bem interessantes sobre cada tipo de função, e para isso usaremos o Geogebra. Se ainda não conhece, entre, crie suas funções e divirta-se vendo como cada uma se comporta. 🙂
Selecione aqui o conteúdo que deseja ver!
Funções trigonométricas
Trigonometria é um nome que dá medo só de ouvir, mas como veremos aqui, as funções trigonométricas não são tão difíceis assim. Dentre as principais, temos as funções: seno, cosseno e tangente. E só para despertar sua curiosidade, há outras funções trigonométricas, porém, veremos apenas as mais comuns no Ensino Médio.
Antes de olharmos os gráficos e as funções em si, saiba que as funções trigonométricas são periódicas, ou seja, possuem um padrão que se repete em determinados intervalos.
– Função seno
A função seno se repete a cada período de 2pi (aproximadamente 6,28), é expressa por f(x) = sen(x) e é limitada entre -1 e 1. Olhe como é o gráfico:
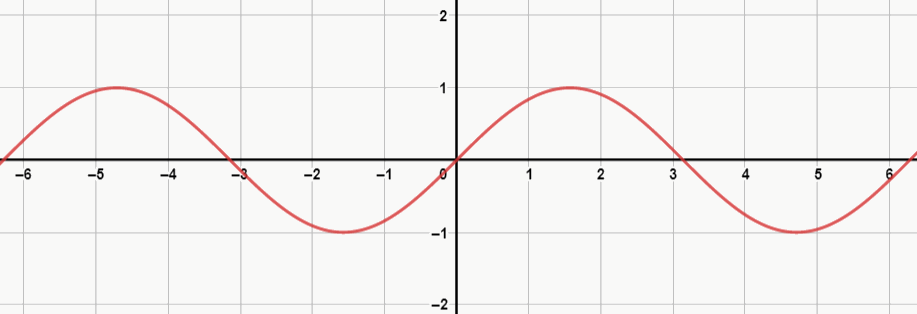
Perceba que o gráfico da função seno passa pela origem do plano.
Curiosidade: os sons que escutamos são nada mais nada menos que ondas sonoras. Desse modo, a música pode ser transformada em funções seno (que formam curvas chamadas de senóides). Esse tipo de onda é bem recebida pelos ouvidos humanos, de modo que a utilização delas é útil na hora de harmonizar determinado ritmo, para que ele “soe bem aos ouvidos”.
– Função cosseno
A função cosseno se repete a cada período de 2pi (aproximadamente 6,28), é expressa por f(x) = cos(x) e é também limitada entre -1 e 1. Olhe como é o gráfico:
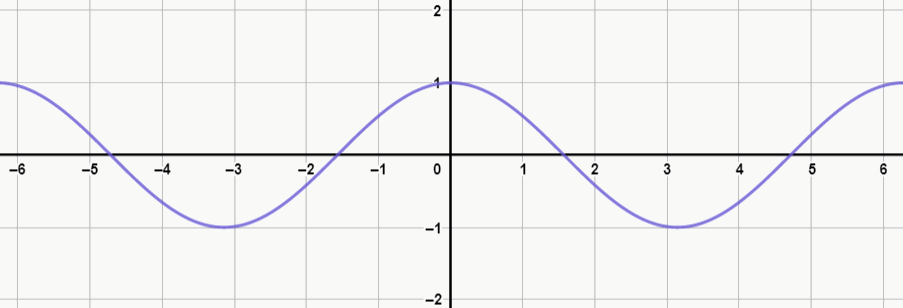
Essa função é bem parecida com a seno, né? Porém, perceba que o gráfico começa em 1, pois o cosseno de 0 é 1. Portanto, como as curvas do seno e cosseno são bem semelhantes, uma dica para fixar qual é qual é lembrar que o seno de 0 é 0 (por isso o gráfico começa na origem) e que o cosseno de 0 é 1 (por isso o gráfico inicia-se em 1). 😉
– Função tangente
A função tangente se repete a cada período de pi (aproximadamente 3,14) e é expressa por f(x) = tg(x). No entanto, esta não possui limites e segue tanto para o infinito positivo quanto para o negativo. Olhe como é o gráfico:
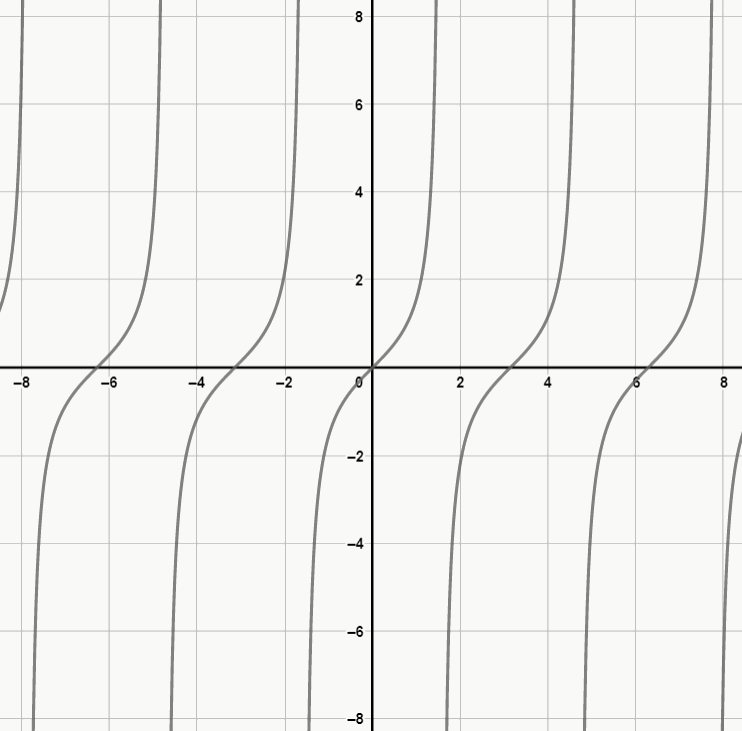
Por fim, vamos ver algumas aplicações?