Equações e Inequações
Equações e inequações são nomes bem parecidos, porém, isso não significa que tenham significados semelhantes.
Quando escrevemos uma equação, estamos criando uma igualdade, e por esse motivo, o sinal de igual ( = ) sempre deve aparecer em nossa expressão. Além disso, em uma equação, nosso objetivo é encontrar um ou mais números específicos que satisfaçam nossa expressão matemática. Portanto, em uma equação, uma coisa deve ser obrigatoriamente igual a outra, ou isso não será uma equação.
Já em uma inequação, estamos falando sobre uma desigualdade, e dessa forma, teremos os sinais de maior ( > ), menor ( < ), maior ou igual ( ≥ ) e menor ou igual ( ≤ ) em nossa expressão. O nosso objetivo agora não é encontrar um número específico, mas sim um conjunto de valores que satisfaçam nossa condição de desigualdade. As resoluções das inequações são praticamente iguais às das equações, exceto quando há mais de 1 resposta. Neste caso, você deverá avaliar quais das respostas fazem parte do conjunto solução, como veremos mais à frente.
Selecione aqui o conteúdo que deseja ver!
Inequações do 1° grau
Agora que você já sabe a verdade por trás da frase “passar para o outro lado”, vamos ver como resolver uma inequação.
Inequação 1: 3x – 7 > 5
Antes de resolvê-la, vamos interpretar esta expressão. O que queremos aí é um conjunto de números para que a expressão 3x – 7 seja maior que 5. Então vamos resolver!
Isolando novamente o x, temos que:
Dessa forma, vemos que para que a expressão 3x – 7 seja maior que 5, é necessário um número maior que 4.
Inequação 2: 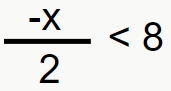
Isolando x, encontramos que:
-x < 2*8 → -x < 16
Deixar a incógnita com o sinal negativo, apesar não ser errado, não é algo muito comum, então para consertar isso, basta multiplicar ambos os lados por -1 para obter:
x < -16
Tá certo isso aí? Não, faltou fazer alguma coisa, pois se você substituir x por um número menor que -16, como por exemplo, -16,1, verá que teremos 8,05 como resposta, e isso é maior que 8. Portanto, nossa resposta está errada.
O que fizemos de errado então? Sempre que você multiplicar uma inequação por -1, você deve obrigatoriamente inverter o sinal da desigualdade. No nosso caso, o sinal de menor ( < ) deve se tornar um sinal de maior ( > ). Fazendo isso, temos agora que:
x > -16
Teste agora um número maior que 16, (por exemplo -15,9) para ver o que acontece. O resultado é 7,95, que é menor que 8. Portanto, para que a expressão -x/2 seja menor que 8, é necessário um número que seja maior que -16.