As operações fundamentais

As 4 operações fundamentais da matemática são as bases para qualquer tipo de cálculo que desejamos fazer. Sendo assim, vamos dar uma olhada em alguns fatos curiosos sobre elas e observar, através de uma pequena história, como as utilizamos no dia a dia sem nem menos perceber.

Multiplicação e Divisão

Origem dos sinais: Na escola, antes de aprendermos as equações com incógnitas (que são valores desconhecidos), era comum usarmos o X para representar uma multiplicação. Mas, depois que a variável x entra em cena, passamos a utilizar o símbolo ( . ) para representar essas operações. Algo interessante de se notar é que, no meio computacional, utilizamos o asterisco ( * ) para representar essa operação.

O símbolo X foi utilizado pela primeira vez em 1631, porém, pelo mesmo motivo citado anteriormente, foi substituído pelo ponto ( . ).

Na divisão, a representação a/b foi criada pelos árabes, já a utilização do símbolo ( : ) foi feita apenas em 1657 pelo inglês William Oughtred. E o sinal mais conhecido (÷) foi desenvolvido a partir da junção da barra ( / ) dos árabes e os dois pontos ( : ) de Oughtred.

Curiosidade: divisão por 0

Bem, você sabe que 0 dividido por qualquer número é sempre 0, não é mesmo? Pois afinal, não temos como dividir o nada em várias partes.

Mas você já tentou dividir algo por zero? Isso pode causar certa confusão, então vamos dar uma olhada. Ao ler a pergunta, você pode ter pensado: “muito fácil, um número dividido por 0 é igual a 0 pois não dá para dividir algo pelo nada”. Na verdade, uma divisão por zero resulta no que chamamos de indeterminação, e você pode pensar nisso como sendo algo que é impossível de ser encontrado e que não é um número.

Mas para entender o conceito matemático dessa indeterminação, vamos olhar para as imagens abaixo:

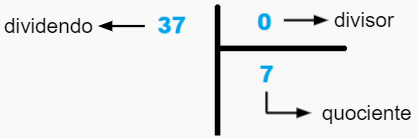
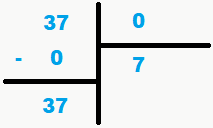
Primeiramente, devemos lembrar como funciona uma divisão pelo método das imagens.

E é isso, este é o significado matemático por trás das divisões por 0 e porque não temos como resolvê-las. Vale ressaltar que existem outros tipos de indeterminações na matemática, mas essas aparecem com mais frequência no ensino superior.

Curiosidade: os nomes especiais

Durante as aulas de matemática você já deve ter ouvido falar de produto, quociente, oposto e inverso. Mas o que significam esses nomes?

Um produto refere-se ao resultado da multiplicação entre dois números, já o quociente refere-se ao resultado de uma divisão.

Quando pensamos no oposto de um número, estamos basicamente pensando no mesmo número, só que com o sinal contrário. Exemplos: 3 e -3; -10 e 10.

Já ao falarmos do inverso, estamos apenas invertendo os valores do numerador com o do denominador. Por exemplo, o inverso de 7/5 é 5/7. Mas e em um valor inteiro, como por exemplo: 4? Lembre-se que os números inteiros também possuem denominadores, mas no caso deles, é sempre 1, ou seja, o número 4 é o mesmo que 4/1, então seu inverso é 1/4.

Matematicamente falando, ao obtermos o inverso de um número, estamos na verdade dividindo 1/n, sendo n um número qualquer. Lembra da regrinha que nos diz o que fazer quando temos uma fração sobre outra? Ela diz que: “deve-se multiplicar o primeiro termo (numerador) pelo inverso do segundo (denominador)”. Pegando os mesmo exemplo anteriores, temos que:

Entendeu? Portanto, agora sempre que ler ou ouvir cada um desses termos, você já sabe o que fazer.