Os números…

Olá, se você chegou até aqui, é porque quer ficar um pouco mais íntimo dos números. Neste módulo, você terá o privilégio de conhecer onde vivem, o que comem, e o que fazem os números… Na verdade, não, pois nós não conseguimos essas informações, uma vez que os números são um pouco tímidos e reservados.

No entanto, conseguimos conversar e entender sobre suas emoções, sua personalidade, e até mesmo sobre suas famílias. Ficou curioso? Farei um resumo para você das informações que conseguimos durante as entrevistas.

Agora, vamos falar sobre família. Aparentemente, os números não possuem muitas palavras para se referir aos seus familiares. Durante as entrevistas, eles se referiram a todos como “primos”.

Os números primos

O conceito de número primo é bem simples: 

• Deve ser um número natural;
• E ter apenas 2 divisores, sendo eles o 1 e o próprio número.

Mas, antes devemos lembrar que:

• Todo número par é divisível por 2;
• Se a soma de todos os algarismos de um número for divisível por 3, o número é divisível por 3;
• Números terminados em 0 e 5 são divisíveis por 5;
• Um número é divisível por 7 se o dobro do último algarismo, subtraído pelo restante do número, resulta em um múltiplo de 7. Ex: 343 –> 2*3 = 6 –> 34 – 6 = 28 –> 28/7 = 4

E se um número não for primo, qual o nome dele?

Os números “não primos” são chamados de compostos, isso porque eles possuem mais de 2 divisores, como por exemplo, o número 10, que pode ser dividido por 1, 2 e 5. Ou seja, possui três divisores.

Bem fácil, né? Vamos ver alguns exemplos:

12:  /1 = 12; /2 = 6; /3 = 4; /4 = 3; /6 = 2 → Portanto, é um número composto, pois, afinal, possui mais de 2 divisores.

11:  /1 = 11; /2 = erro!; /3 = erro!; /5 = erro!; /7 = erro!; /11 = 1 → Como você pode ver, o 11 é divisível apenas por 1 e o próprio 1. Qualquer outro número resultará em um quociente decimal. Portanto, 11 é um número primo.

Agora, apenas para fixar a ideia, realize o exercício a seguir:

Diga se o número é primo ou composto:

Quer saber uma aplicação importantíssima dos números primos na matemática? Aqui vai!

Decomposição em fatores primos

Decompor um número em fatores primos é escrevê-lo como uma multiplicação de números primos. E de acordo com o Teorema Fundamental da Aritmética, todos os números inteiros positivos maiores que 1 podem ser escritos como uma multiplicação de números primos.

Mas onde utilizamos essa decomposição? É muito comum o uso desse artifício quando queremos encontrar o MMC ou MDC de dois ou mais números, além disso, a decomposição é muito utilizada para reescrever raízes não inteiras. Na página sobre equações, utilizamos a decomposição em fatores primos para resolver equações exponenciais.

Mas como decompor um número em fatores primos?

Decompor um número em fatores primos é simplesmente dividir esse número sucessivamente por números primos. Essa divisão é feita em ordem crescente, ou seja, 2, 3, 5, 7, e por aí vai, até que o quociente da divisão seja 1.

Exemplo: decomposição do número 20

Vamos começar as divisões: 20/2 = 10 → 10/2 = 5 → 5/5 = 1. Então temos que 20 = 2*2*5, ou 2² * 5. Vamos organizar tudo isso? Veja a figura a seguir.

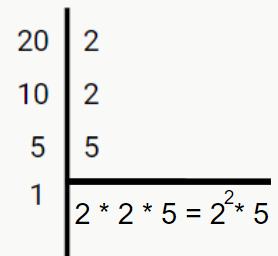
Bem mais fácil de ler agora, né? No fim, é a mesma coisa, só mudou o modo como escrevemos as operações.

Tranquilo, né? Todas as decomposições são iguais, basta ir dividindo por números primos até chegar a 1. Desse modo, que tal fazer alguns exercícios para praticar? Decomponha em fatores primos os seguintes números:

Chegou o momento de falarmos um pouco sobre educação, vamos falar sobre os número educados.