Conjuntos
Conjuntos são utilizados para agrupar coisas. Desse modo, o uso desse conceito vai muito além da matemática e pode ser utilizado em diversos momentos de nossas vidas. Mas como?
Selecione aqui o conteúdo que deseja ver!
Conjuntos numéricos
Um assunto que você já deve ter estudado em suas aulas de geografia é sobre as divisões do país. O Brasil é dividido em 26 estados mais o Distrito Federal; além disso, podemos dividir o país em 5 regiões: Norte, Nordeste, Centro-Oeste, Sudeste e Sul. Cada uma dessas regiões possui características únicas em relação aos seus aspectos sociais, econômicos, físicos e até mesmo culturais.
Mas calma, você não entrou no site errado. Nesse momento você pode estar se perguntando: “O que isso tem a ver com os conjuntos numéricos?”.
E eu te respondo: “Tudo!”
Os conjuntos numéricos são nada mais que agrupamentos de números que possuem características semelhantes. Dentre eles, temos os conjuntos dos números: Naturais, Inteiros, Racionais, Irracionais, Reais e Complexos.
Antes de fazermos uma analogia para você entender melhor a ideia, é necessário introduzir o conceito de subconjunto. Basicamente, um subconjunto é um conjunto menor que faz parte de um conjunto maior, por exemplo, se eu te der esse conjuntos de números: C = {1,2,3,4,5,6} e agrupar todos os pares em um novo conjunto: P = {2,4,6}, e os ímpares em um novo conjunto I = {1, 3, 5}, podemos dizer que os conjuntos P e I são subconjuntos de C, pois todos os números dos nossos conjuntos de pares e ímpares estão contidos em C.
Agora, vamos olhar para as figuras abaixo para você entender melhor onde eu quero chegar ao falar do Brasil:
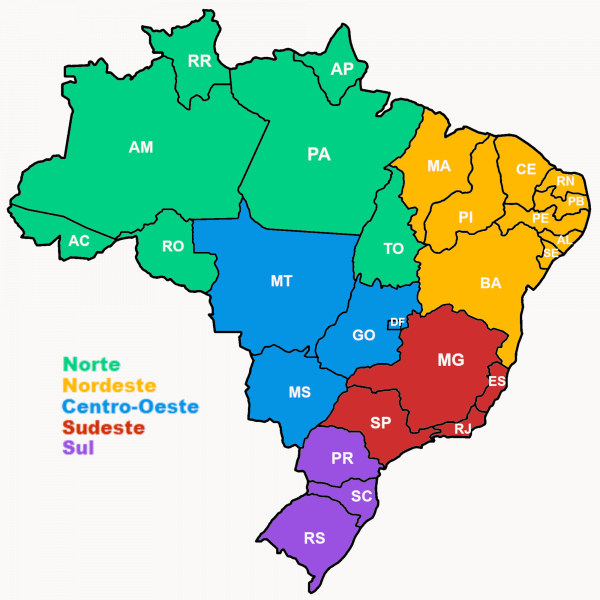
Na figura acima, vemos a divisão do Brasil por regiões e estados. Cada cor representa uma das regiões. Desse modo, podemos construir uma relação entre essas divisões, conforme a imagem a seguir:
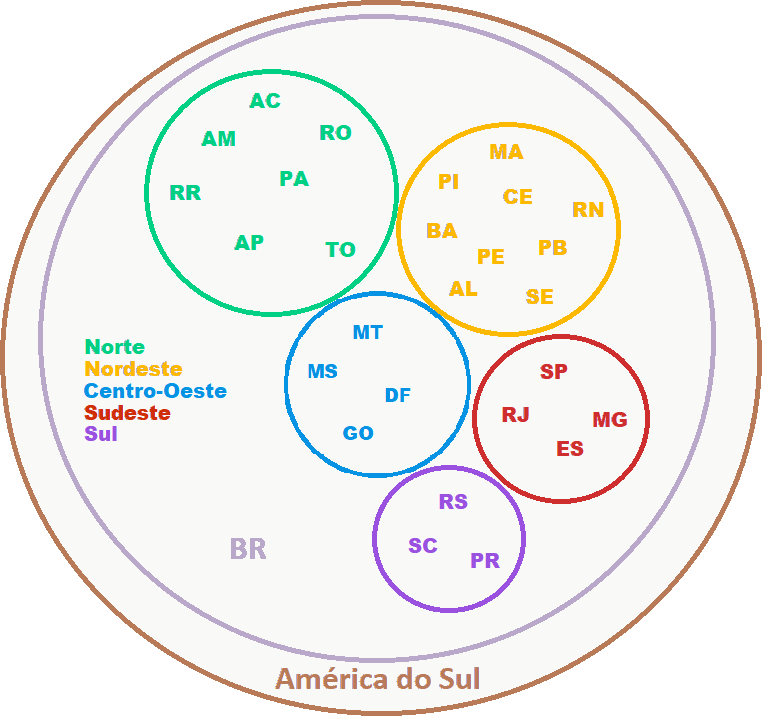
Na figura, podemos perceber que os estados estão divididos em conjuntos, que são as regiões. E podemos ver que essas regiões são subconjuntos de um conjunto maior, que é o Brasil. E o país faz parte de um outro conjunto, que é a América do Sul.
Viu como esse assunto tem tudo a ver com conjuntos?
Mas, agora vamos falar dos conjuntos numéricos em si!
– Os números naturais
Este conjunto foi o primeiro a ser desenvolvido e contém apenas os números inteiros positivos. É representado pela letra N.
Ex: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}
– Os números inteiros
Este conjunto é bem parecido com o dos números naturais, porém, este contém todos os números inteiros, tanto os negativos quanto os positivos. É representado pela letra Z.
Ex: Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}
– Os números racionais
Este conjunto envolve frações formadas por números inteiros. E a partir delas podemos conseguir números decimais.
Mas cuidado! Não são todos os números decimais que estão neste conjunto. Há algumas regras que definem quem faz ou não parte do grupo, que é representado pela letra Q. Essas regras são:
1) Todos os números inteiros fazem parte.
Ex 1: 4/2 = 2
Ex 2: 15/3 = 5
Ex 3: 90/6 = 15
Ex 4: 10/0 = ?
Ops, 0 no denominador não pode, confira o porquê clicando aqui.
2) Números decimais finitos fazem parte.
Ex 1: 2,5 ou 5/2
Ex 2: 3,7 ou 37/10
Ex 3: 0,25 ou 1/4
3) Dízimas periódicas fazem parte: são números decimais infinitos, mas que seguem um padrão numérico em sua infinitude.
Ex 1: 1,33333…
Ex 2: 4,572572…
Ex 3: 15,1919…
– Os números irracionais
Podemos dizer que esse conjunto é um agrupamento dos números que não fazem parte do conjunto dos racionais. Desse modo, o elemento que não for “racional” fará necessariamente parte dos “irracionais”, que é representado pela letra I. É o grupo formado por todos os números que não podem ser escritos como uma fração de dois números inteiros. Podemos então estabelecer que:
1- Raízes não exatas fazem parte deste conjunto.
Ex 1: √2 = 1,41421356237…
Ex 2: √3 = 1,73205080756…
2- Dízimas não periódicas fazem parte: são números decimais infinitos, mas que não seguem um padrão numérico em sua infinitude.
Ex 1: π = 3,1415926535897…
Ex 2: 6,3524678510980…
– Os números reais
Assim como o Brasil é o conjunto que abrange todas as suas regiões, podemos pensar neste conjunto como sendo exatamente isso, um conjunto que contém todos os outros. Desta forma, todos os grupos citados anteriormente fazem parte deste conjunto numérico, que é representado pela letra R.
Ou seja, R = {Q + I}
– Os números complexos
Por fim, há o conjunto dos números complexos. Não vamos entrar em muitos detalhes pois há uma página inteira só para eles. Mas, assim como o conjunto dos reais pode ser visto como o Brasil em relação aos outros grupos, este conjunto pode ser visto como a América do Sul em relação ao Brasil, pois o conjunto dos reais é um subconjunto dos complexos, que é representado pela letra C.
Para finalizar, vamos ver uma imagem que possui ideia semelhante à feita para o Brasil no início da página, mas, desta vez, faremos com os conjuntos numéricos apresentados.

O que a imagem nos diz é:
- O conjunto N (naturais) é subconjunto de Z (inteiros);
- O conjunto Z (inteiros) é subconjunto de Q (racionais);
- Os conjuntos Q (racionais) e I (irracionais) são subconjuntos de R (reais);
- O conjunto R (reais) é subconjunto de C (complexos).
Depois de muito conteúdo, ficou mais claro o que são conjuntos e que esse conceito não serve apenas para números? Da mesma forma que foi feita para o Brasil, você pode criar conjuntos de diversas coisas, pois a finalidade deles é justamente organizar.
Já pensou em organizar suas séries preferidas por tema? Ou talvez formar um conjunto de livros de um mesmo autor, porém com temáticas diferentes, separando-os em vários subconjuntos? Pensa aí e crie seus próprios conjuntos. 😉
Mas o assunto não para por aí, vamos ver agora como realizar operações entre os conjuntos.