Números Complexos

Os números complexos, também conhecidos como números imaginários, são números que não existem no mundo real, mas nem por isso eles deixam de ser importantes. Na página sobre conjuntos numéricos, falamos um pouco sobre esse conjunto e dissemos que ele abrange todos os números reais. Mas então, o que mais eles têm a oferecer?

Os números complexos são formados por duas partes, sendo uma real e uma imaginária. A real é representada por um número real, já a imaginária é formada pela multiplicação entre um número qualquer e o símbolo i.

Chamando o número complexo de “z”, segue que:

 sendo a e b números reais e i a unidade imaginária

Esse tipo de numeral foi criado com um objetivo: encontrar soluções para equações polinomiais de segundo e terceiro grau que resultam em raízes quadradas de números negativos. Mas qual o valor de i?

• i¹ = i =
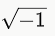
• i² = -1
• i³ =  -i
• i⁴ = 1

Se quiser saber como cada valor de i foi encontrado, confira o vídeo “Números Complexos – Noções básicas” do canal Marcos Aba Math teacher.

Beleza, mas como utilizar o i?

Vamos supor que você esteja resolvendo uma equação de segundo grau, e no momento que calcula o valor do delta, com a fórmula b² – 4 * a * c, encontra o valor -81 como resultado.

Você sabe que agora terá que usar a fórmula de Bhaskara 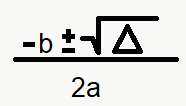. Porém, seu delta é um número negativo, e sabemos que não existe raiz real de número negativo.

Em outra página do ramo da Aritmética, falamos sobre as operações fundamentais da matemática, e elas continuam valendo para os números complexos. Caso queira saber mais sobre essas operações, recomendo a playlist “Números Complexos” do canal Marcos Aba Math teacher.

Aplicações dos números complexos

Como você viu, os números complexos foram criados com o princípio de oferecer soluções para raízes de números negativos. Em geral, as aplicações são voltadas para as engenharias:

• elétrica, na parte de circuitos elétricos; 
• e de controle, como por exemplo, no controle da quantidade de água e taxa de saída ou no controle de temperatura de tanques e fornos, onde o sinal da parte real do número complexo encontrado a partir de uma equação de segunda ordem (ou segundo grau) serve para determinar o comportamento do sistema ao longo do tempo. Dessa forma, esses números ajudam a encontrar os sistemas mais eficientes e melhor controlados.

Para mais informações sobre essas aplicações, acesse a monografia “Números Complexos”, realizada por estudantes da Licenciatura em Matemática na UNICAMP.