Conjuntos
Conjuntos são utilizados para agrupar coisas. Desse modo, o uso desse conceito vai muito além da matemática e pode ser utilizado em diversos momentos de nossas vidas. Mas como?
Selecione aqui o conteúdo que deseja ver!
Operações com conjuntos
Após aprender sobre os conceitos básicos que compõem a Teoria dos Conjuntos e como utilizar a ideia de conjunto no cotidiano, vamos estudar as possíveis operações entre dois conjuntos. Existem 4, e são elas: união, intersecção, diferença de conjuntos e conjunto complementar.
– União
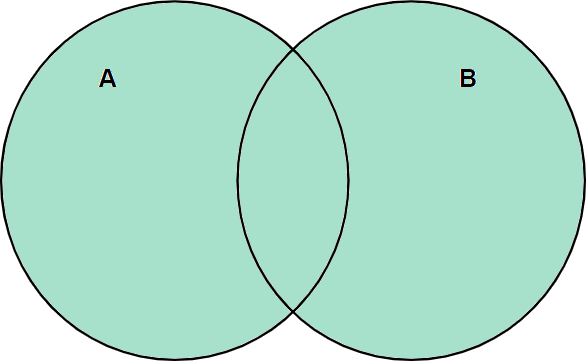
A operação de união de conjuntos é bem simples. Dados dois conjuntos A e B, basta pegar todos os elementos de A e juntar com os elementos de B, ou vice-versa. A operação é indicada com o símbolo U.
Exemplo 1: A = {2, 4, 6, 8}, B = {1, 3, 5, 7}
- A U B = {1, 2, 3, 4, 5, 6, 7, 8}
- B U A = {1, 2, 3, 4, 5, 6, 7, 8}
Note, contudo, que caso um ou mais elementos pertençam aos dois conjuntos, eles não devem aparecer duas vezes no conjunto formado pela união, justamente por serem elementos repetidos, e isso valerá para qualquer uma das operações.
Exemplo 2: C = {d, g, h, k}, D = {d, e, f, g}
- C U D = {d, e, f, g, h, k}
- D U C = {d, e, f, g, h, k}
Dados dois conjuntos A e B, também podemos representar a união por meio do seguinte diagrama.
– Intersecção
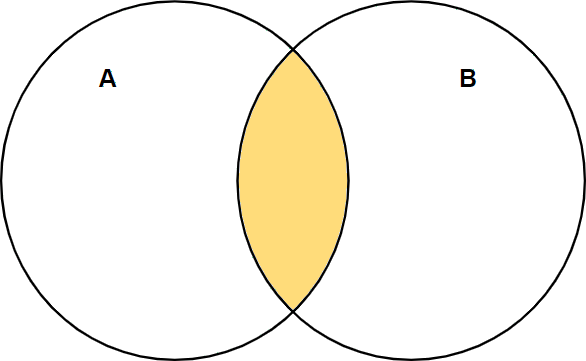
A operação de intersecção consiste em juntar os elementos comuns de dois conjuntos para formar um novo conjunto. A operação é indicada com o símbolo ∩. Ou seja, dados dois conjuntos A e B, ao fazer A∩B, devemos olhar os elementos de A e ver quais deles se repetem em B. Da mesma forma, podemos fazer B∩A que teremos o mesmo resultado. Feito isso, basta criar um novo conjunto com esses elementos repetidos. Se dois conjuntos não tiverem elementos em comum, o resultado é um conjunto vazio, representado por Ø ou { }.
Exemplos: A = {2, 4, m, 8}, B = {a, 3, 5, 7}, C = {a, 4, m, 7}
- A∩C = {4, m}
- C∩A = {4, m}
- B∩C = {a, 7}
- B∩A = {Ø}
Dados dois conjuntos A e B, também podemos representar a intersecção por meio do seguinte diagrama.
– Diferença de conjuntos
Nessa operação ocorre o contrário da intersecção, pois aqui devemos olhar os elementos comuns entre os dois conjuntos e excluí-los do novo conjunto formado. A operação é indicada com o símbolo – . Ou seja, dados dois conjuntos A e B, ao fazer A – B, devemos tirar de A tudo aquilo que for comum com B. Mas ainda não ficou muito claro, né? Vamos ver alguns exemplos para entendermos melhor.
Sejam os conjuntos A = {2, 4, 6, 8}, B = {1, 3, 5, 7}, C = {1, 4, 6, 7}
- Exemplo 1: A – B = {2, 4, 6, 8}
- Exemplo 2: B – A = {1, 3, 5, 7}
- Exemplo 3: B – C = {3, 5}
- Exemplo 4: C – B = {4, 6}
No exemplo 1, temos A – B, então devemos pegar o conjunto A, olhar os elementos que também estão em B, para então excluí-los de A e formar um novo conjunto. Como não há elementos em comum, basta repetir os elementos de A.
No exemplo 2, temos B – A. Note que o resultado muda! Desse modo, como sabemos que A e B não possuem elementos em comum, basta repetir os elementos de B no novo conjunto.
No exemplo 3, temos B – C. Se olharmos para os dois conjuntos, vemos que os elementos 1 e 7 são comuns entre ambos, portanto, basta excluí-los de B para chegar no resultado {3, 5}.
Por fim, no exemplo 4, temos C – B. E como já sabemos que 1 e 7 são comuns entre B e C, basta retirar esses elementos de C para chegar na resposta {4, 6}.
Dados dois conjuntos A e B, também podemos representar a diferença por meio do seguinte diagrama.
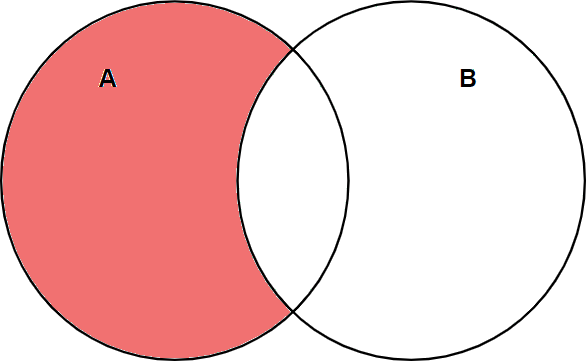
Pense aí, seguindo os moldes do diagrama acima, qual seria o diagrama formado por B – A? 🤔
Importante! Em cada um dos tópicos acima, foram resolvidos exemplos em que somente uma operação foi utilizada. Contudo, podemos utilizar todas elas em uma única expressão. Nesses casos, você deve resolvê-la seguindo linearmente a expressão fornecida. Vamos ver alguns exemplos utilizando os mesmos conjuntos A, B e C vistos anteriormente.
Sejam os conjuntos: A = {2, 4, 6, 8}, B = {1, 3, 5, 7}, C = {1, 4, 6, 7}. Vamos determinar:
- AUB∩C
Primeiramente devemos fazer AUB. Desse modo, temos que AUB = {1, 2, 3, 4, 5, 6, 7, 8}.
Agora, utilizando o conjunto formado pela união entre A e B (AUB), devemos fazer a intersecção com C, chegando ao conjunto {1, 4, 6, 7}.
- A∩C-B
Primeiramente devemos fazer A∩C. Desse modos, temos que A∩C = {4, 6}.
Agora basta pegar esse conjunto que encontramos (A∩C) e aplicar a operação de diferença com B. Ao fazer isso, percebe-se que o conjunto A∩C não possui elementos em comum com B. Portanto, basta repetir o conjunto A∩C, ou seja, {4, 6}.
- A-C∩B
Primeiro subtraímos A-C. Desse modo, temos que A-C = {2, 8}.
Agora temos que pegar esse conjunto (A-C) e fazer a intersecção com B. Fazendo isso, vemos que não há elementos comuns entre ambos os conjuntos. Portanto, temos que A-C∩B = Ø
– Conjunto complementar
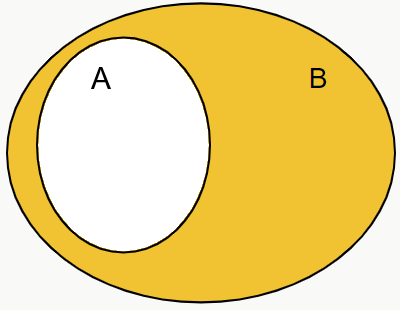
O conjunto complementar é uma operação que depende da perspectiva pela qual observamos o problema, pois o complemento de um conjunto pode ser em relação ao conjunto universo ou a um outro conjunto mais restrito.
Quando o complemento for em relação ao conjunto universo, dado um conjunto A, será representado por AC.
Quando for em relação a um outro conjunto, dados dois conjuntos A e B, o complementar de A em relação a B será representado pela notação 
Exemplos:
- Dado o conjunto dos números ímpares A = {1, 3, 5, 7, 9, …}, o complemento em relação ao conjunto universo dos números naturais é o conjunto dos números pares {0, 2, 4, 6, 8, …}.
- Dado o conjunto das vogais V = {a, e, i, o, u}, o complemento em relação ao conjunto universo do alfabeto é o conjunto das consoantes.
- Dado os conjuntos A = {1, 2, 3, 4, 5, 6} e B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, o complementar de A em relação a B é o conjunto B – A = {7, 8, 9, 10}.
Dado um conjunto A, podemos representar o conjunto complementar de A em relação ao universo e a um outro conjunto mais restrito das seguintes maneiras.
Mas o que são esses diagramas que utilizamos para representar as operações? Vamos descobrir juntos!