Estudo de cônicas
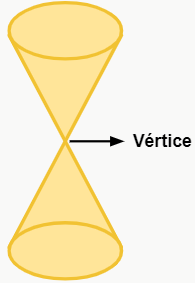
Cônicas são figuras geométricas formadas a partir do chamado cone duplo de revolução, que consiste, de maneira bem informal, em “dois cones retos ligados verticalmente pelo vértice”, como ilustra a figura a seguir. Para obter as cônicas, é necessário fazer alguns “cortes” nesse cone, como veremos adiante. Fazendo isso, obtemos as seguintes figuras: elipse, hipérbole, parábola e circunferência.
Elipse
A elipse é uma figura gerada a partir de um corte não reto em qualquer sentido do cone, como mostra a figura a seguir:

Colocando a elipse em um plano, podemos destacar alguns pontos importantes que encontramos na figura e que serão muito úteis na realização de cálculos.
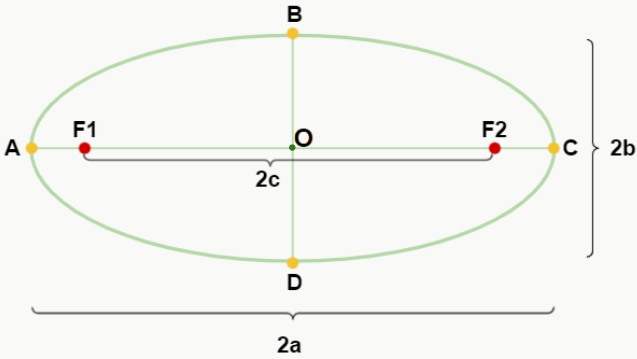
Onde A, B, C e D são os vértices da elipse, F1 e F2 são os focos, 2a é o tamanho do eixo maior, 2b é o tamanho do eixo menor, 2c é a distância entre os focos e O é o centro da elipse. Cabe ressaltar que os focos da elipse estão sempre posicionados no eixo maior.
Mas, e se eu não tiver essa figura em mãos, como saber se ela é mesmo uma elipse? Para isso, devemos observar se a seguinte relação é verdadeira:
d(PF1) + d(PF2) = 2a
Ou seja, a distância de um ponto P da elipse até o foco F1 somado à distância desse mesmo ponto P até o foco F2 deve ser igual a 2a, que é a medida do eixo maior.
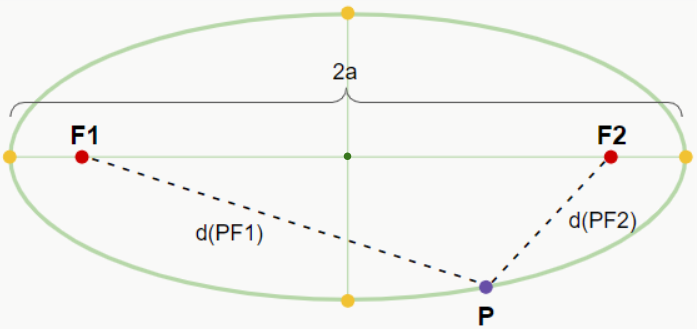
Um outro detalhe sobre a elipse é o fato de que podemos formar um triângulo retângulo utilizando os segmentos OB, OC e BF2. Note que este mesmo triângulo pode ser formado nas outras partes da elipse. Mas qual a importância disso? Observe a figura a seguir:
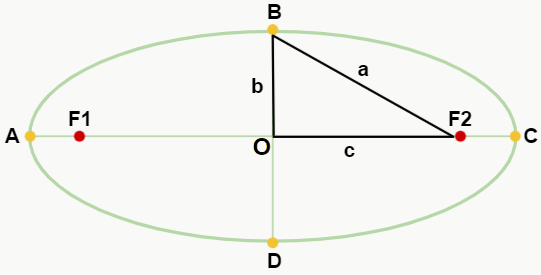
Note que de novo temos uma medida a na imagem, que agora representa a hipotenusa do triângulo retângulo OBF2. Antes, vimos que 2a era igual à distância entre os vértices A e C. Portanto, concorda que a corresponde à distância entre o centro O e os vértices A ou C? Sendo assim, temos aqui uma informação muito importante e que pode nos ajudar a resolver diversos problemas envolvendo elipses, pois, como o triângulo é retângulo, podemos utilizar o Teorema de Pitágoras (a2 = b2 + c2) para encontrar os valores de a, b e c.
Ok, mas onde e como utilizar todos esses pontos (vértices, focos e eixos) da elipse? Iremos utilizar todos esses elementos para formar a chamada equação da elipse. O interessante é que há dois tipos de equação: uma quando os focos estão sobre o eixo x, e outra quando os focos estão sobre o eixo y.
Sobre o eixo x:
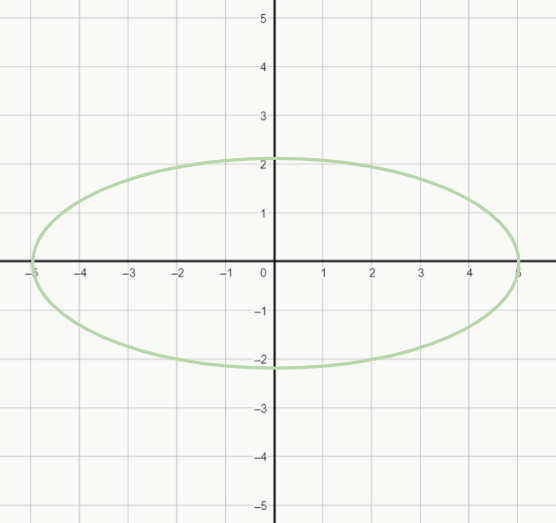
Sobre o eixo y:
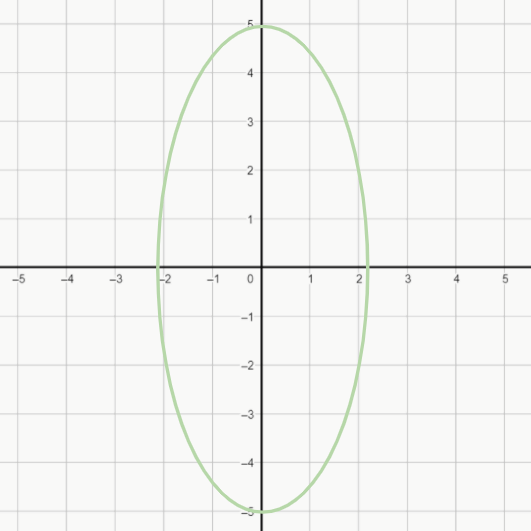
Nessas equações, a é a distância entre o centro e o ponto mais distante da elipse (metade do eixo maior), e b é a distância entre o centro e o ponto menos distante (metade do eixo menor). Já x e y são quaisquer coordenadas da figura.
Ainda há outras figuras para estudarmos. Sendo assim, que tal avançar para a próxima página?