Estudo da Circunferência
Podemos definir uma circunferência como um conjunto de pontos que possuem a mesma distância (são equidistantes) de um ponto central C (conhecido como “centro da circunferência”). Assim como a elipse, a hipérbole, e a parábola, a circunferência também é uma figura cônica e, portanto, pode ser obtida através de um corte paralelo à base do chamado cone duplo de revolução.
Selecione aqui o conteúdo que deseja ver!
Equação da Circunferência
Assim como tudo na geometria analítica, a circunferência também pode ser representada por uma equação que nos permite descobrir várias características importantes sobre a circunferência, como o centro, a medida do raio e os pontos pertencentes à figura. Mas como é essa equação?
A chamada equação reduzida da circunferência é a seguinte:
(x – xc)2 + (y – yc)2 = r2
Onde x e y são as coordenadas de um ponto qualquer da circunferência, xc e yc são as coordenadas do centro, e r é o raio.
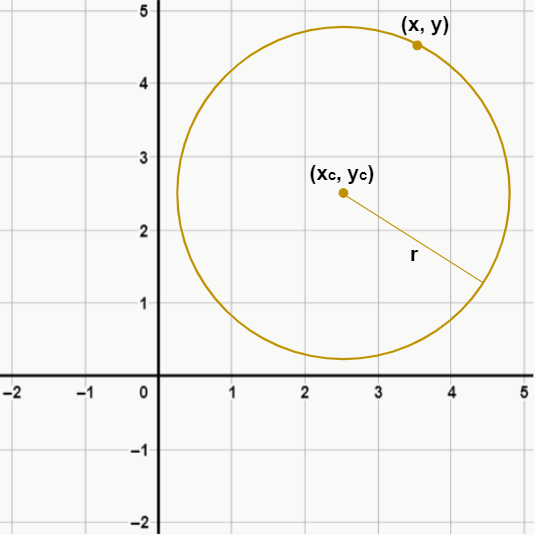
Note que a equação da circunferência parece muito com o Teorema de Pitágoras. Vamos ver por quê? Observe a figura a seguir:
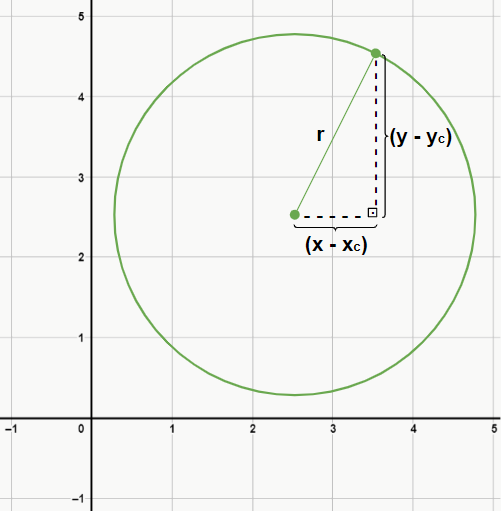
Perceba que, ao adicionar na figura (x – xc), que corresponde à distância entre os pontos no eixo x, e (y – yc), que corresponde à distância entre os pontos no eixo y, é possível formar um triângulo retângulo. E quem é a hipotenusa desse triângulo? Justamente o raio r da circunferência. Aplicando o Teorema de Pitágoras para esse triângulo você chegará na equação da circunferência 😉.
Uma parte importante que devemos nos atentar na equação reduzida é em relação às coordenadas do centro. Note que, na frente de xc e yc aparece o sinal de menos (-), ou seja, se a equação aparece com o sinal negativo, é porque a coordenada é positiva, e se aparece com o sinal positivo, é porque a coordenada é negativa. Da mesma forma, perceba que o raio está sempre elevado ao quadrado, mesmo quando esse “quadrado” não aparece explicitamente na equação. Vamos treinar um pouco.
Ex. 1: identifique o centro e o raio da circunferência a partir de sua equação reduzida:
a) (x – 3)2 + (y – 6)2 = 16
Se o sinal é negativo, então as coordenadas do centro são positivas. Desse modo, temos uma circunferência de centro C = (3, 6). E o raio? Temos ali o valor 16, porém, lembre-se que isso é resultado de “algo” que foi elevado ao quadrado. Desse modo, para descobrir quem é este “algo”, temos que tirar a raiz quadrada do número. E como sabemos, a raiz quadrada de 16 é 4. Portanto, o raio da circunferência é 4.
b) (x + 5)2 + (y + 1)2 = 100
Se o sinal é positivo, então as coordenadas são negativas. Desse modo, temos uma circunferência de centro C = (-5, -1). Para descobrir o raio, basta tirar a raiz quadrada de 100, que é 10.
c) (x – 10)2 + (y + 4)2 = 72
Baseando-se nos exemplos anteriores, temos uma circunferência de centro C = (10, -4). Neste caso, perceba que o “quadrado do raio” aparece na expressão, ou seja, o raio é igual a 7. Se quiser, pode tirar a raiz quadrada de 72 também, pois o resultado será 7 da mesma forma.
O interessante sobre a equação reduzida é que, a partir dela, podemos encontrar uma outra, chamada equação geral da circunferência. Para isso, precisamos “abri-la” utilizando os produtos notáveis em (x – xc)2 e (y – yc)2, ou seja:
(x – xc)2 + (y – yc)2 = r2
(x2 – 2xcx + xc2 ) + (y2 – 2ycy + yc2 ) = r2
x2 + y2 – 2xcx – 2ycy + xc2 + yc2 – r2 = 0
Mas, e se eu não sei qual é a equação reduzida, como encontrar a geral?
Nesse caso, não sabendo qual é a equação reduzida, temos que construí-la. E para isso precisamos ou saber quais são as coordenadas do centro e o valor do raio, ou ter um gráfico sobre a circunferência. Vamos fazer um exemplo de cada para entender melhor?
Ex. 2: dada uma circunferência de centro C = (-1, 3) e raio r = 3, encontre sua equação geral.
Como sabemos as coordenadas do centro e o valor do raio, basta substituirmos esses valores na equação reduzida.
(x + 1)2 + (y – 3)2 = 32
Feito isso, temos que “abrir” a equação aplicando os produtos notáveis.
x2 – 2*(-1)*x + (-1)2 + y2 – 2*3*y + 32 =9
x2 + y2 + 2x – 6y + 1 + 9 = 9
x2 + y2 + 2x – 6y + 10 = 9
x2 + y2 + 2x – 6y + 1 = 0
Ex. 3: dada a imagem a seguir, encontre a equação geral da circunferência.
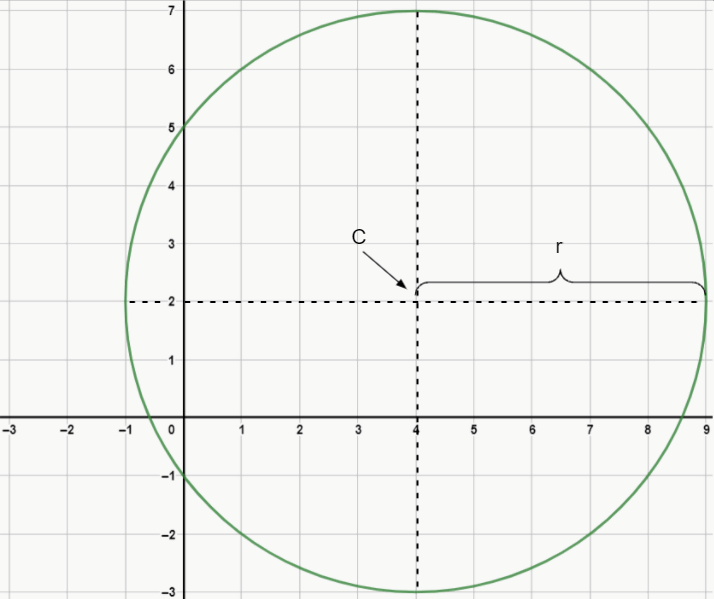
Olhando para a imagem, verifica-se que a circunferência possui centro em C = (4, 2), e raio que vai de 4 a 9, ou seja, r = 5.
Sabendo dessas informações, é só construir a equação reduzida e aplicar os produtos notáveis.
(x – 4)2 + (y – 2)2 = 52
x2 – 2*4*x + 42 + y2 – 2*2*y + 22 = 25
x2 + y2 – 8x – 4y + 16 + 4 = 25
x2 + y2 – 8x – 4y + 20 = 25
x2 + y2 – 8x – 4y – 5 = 0
Mas se eu consigo uma equação a partir da outra, qual a diferença entre elas? Elas são, de fato, equivalentes, pois uma é apenas a expansão da outra. Porém, a diferença entre elas é que a equação geral é mais útil quando queremos calcular as coordenadas do centro e o raio da circunferência, pois podemos utilizar o chamado método da comparação. Nesse método, iremos pegar a equação geral de uma circunferência já conhecida e comparar com a equação geral de uma circunferência qualquer. Olha só:
Ex. 4: calcule as coordenadas do centro e o raio de uma circunferência de equação geral x2 + y2 + 3x – y – 7 = 0.
De acordo com o método da comparação, devemos comparar a equação geral de uma circunferência conhecida com a equação geral de uma circunferência qualquer (x2 + y2 – 2xcx – 2ycy + xc2 + yc2 – r2 = 0). Mas como é feita esta comparação?
Para encontrar as informações que queremos, iremos comparar os termos em comum das duas equações, ou seja, x com x, y com y e termo independente com termo independente:
3x = -2xcx
-y = -2ycy
-7 = xc2 + yc2 – r2
Começando com xc:
3x = -2xcx
3 = -2xc
-3/2 = xc
Continuando com yc:
-y = -2 yc y
y = 2 yc y
1/2 = yc
Sabendo quanto valem xc e yc, podemos descobrir o valor do raio:
Portanto, temos uma circunferência de centro C = (-3/2, 1/2) e de raio r = 3,1.
Viu como é simples? A partir de um único método conseguimos descobrir diversas coisas sobre a circunferência. Sabendo disso, vamos continuar nosso estudo?
Referências
Equação da circunferência
https://mundoeducacao.uol.com.br/matematica/equacao-normal-circunferencia.htm
https://brasilescola.uol.com.br/matematica/equacao-normal-circunferencia.htm