Estudo do Ponto e Reta

O estudo do ponto e da reta é fundamental para a geometria, pois esses elementos constituem a base de toda a disciplina. Além disso, podemos utilizá-los para descobrir informações importantes sobre diversas figuras geométricas, como a circunferência, por exemplo.

Equação geral da reta

Uma reta pode ser definida por uma equação, chamada de equação geral da reta. Essa equação é apresentada a seguir:

ax + by + c = 0

Onde a, b e c são, respectivamente, os coeficientes de x, y e do termo independente. Além disso, a e b não podem ser, ao mesmo tempo, iguais a 0.

Mas como chegamos a essa equação? Para encontrá-la, temos que utilizar matrizes.

Como visto na página anterior, uma reta pode ser definida por dois pontos (x₁, y₁ e x₂, y₂). Desse modo, montando uma matriz 3×3 com esses dois pontos e um terceiro ponto qualquer da reta (x, y), e calculando o determinante dessa matriz, podemos encontrar a equação geral da reta.

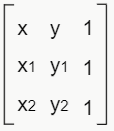
Calculando o determinante, iremos encontrar:

(y₁ – y₂) x + (x₂ – x₁) y + (x₁y₂ – x₂y₁) = 0

Ué, mas isso não parece com a equação mostrada no início da página… Na verdade, elas são exatamente a mesma equação, porém precisamos olhá-la a partir de uma perspectiva diferente. Perceba que, assim como a primeira equação, esta é também dividida em três “partes”, sendo uma de índice x, outra de índice y e outra sem nenhum índice, ou seja, é um termo independente. Viu alguma similaridade?

Chamando cada um desses termos de a, b e c, ou seja, a = (y₁ – y₂), b = (x2 – x1) e c = x₁y₂ – x₂y₁, temos que:

ax + by + c = 0

Que é exatamente a equação geral da reta! Dessa forma, através de uma matriz e dois pontos, podemos descobrir a equação de geral de qualquer reta do plano cartesiano 😄.

Agora que já sabemos como encontrar equações que definem retas, vamos aprender mais sobre elas!

Referências

Equação da reta

https://www.todamateria.com.br/equacao-da-reta/

https://www.infoescola.com/geometria-analitica/equacoes-da-reta/