Estudo de cônicas
Cônicas são figuras geométricas formadas a partir do chamado cone duplo de revolução, que consiste, de maneira bem informal, em “dois cones retos ligados verticalmente pelo vértice”, como ilustra a figura a seguir. Para obter as cônicas, é necessário fazer alguns “cortes” nesse cone, como veremos adiante. Fazendo isso, obtemos as seguintes figuras: elipse, hipérbole, parábola e circunferência.
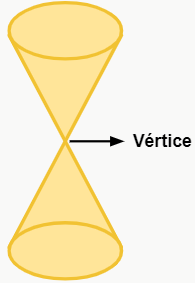
Parábola
A parábola é uma figura gerada a partir de um corte vertical que passa pela base do cone, como mostra a figura a seguir:
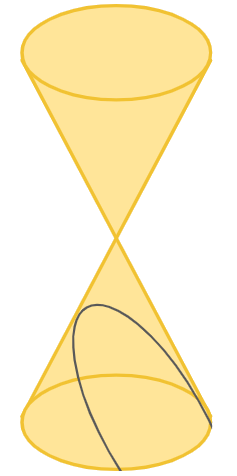
Colocando a parábola em um plano, podemos verificar alguns pontos de destaque da figura.
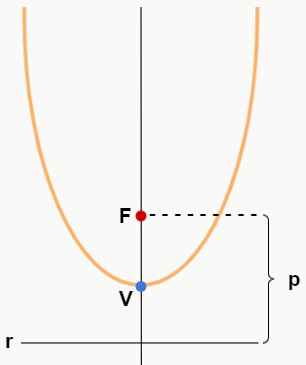
Onde F é o foco da parábola, V é o vértice da parábola, r é a chamada reta diretriz, e p é a distância entre o foco e a reta diretriz.
É importante destacar que a distância da reta diretriz para o vértice da parábola é sempre igual à distância do foco para o vértice da parábola.
Sabendo disso, podemos então definir uma condição de existência para a parábola, que consiste em:
d(PF) = d(Pr)
Ou seja, a distância de um ponto P da parábola ao foco F deve ser igual à distância entre esse mesmo ponto P à reta diretriz r.
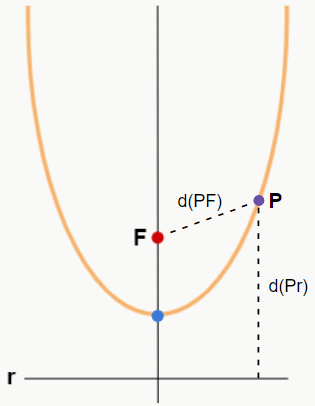
Sendo assim, a partir desses pontos, podemos escrever a equação da parábola, que irá se modificar conforme a posição da parábola no plano cartesiano, conforme as figuras a seguir.
Concavidade para cima:
x2 = 2py
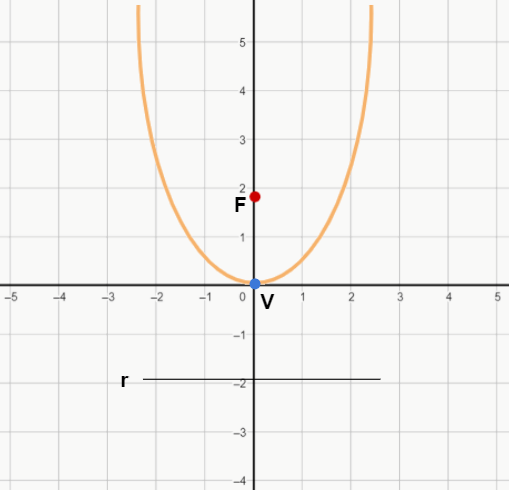
Concavidade para baixo:
x2 = -2py
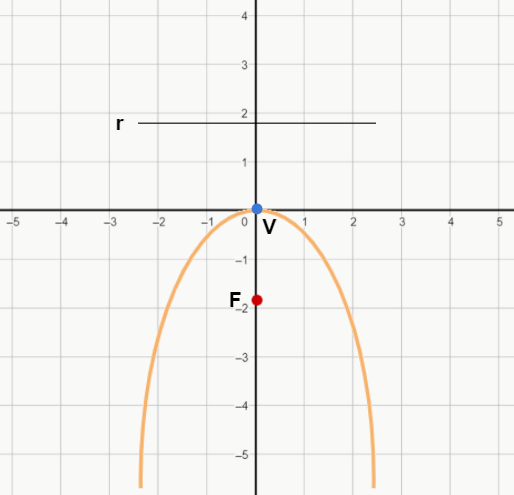
Concavidade para a direita:
y2 = 2px
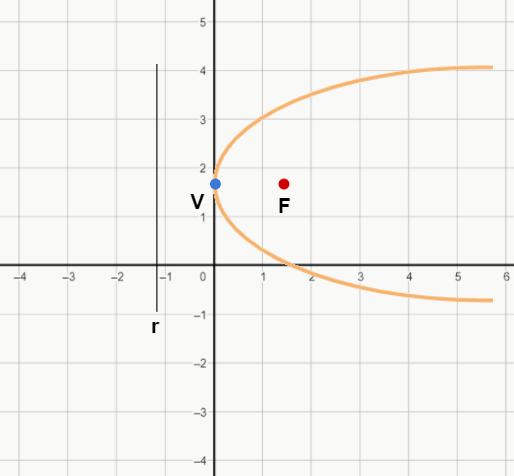
Concavidade para a esquerda:
y2 = -2px
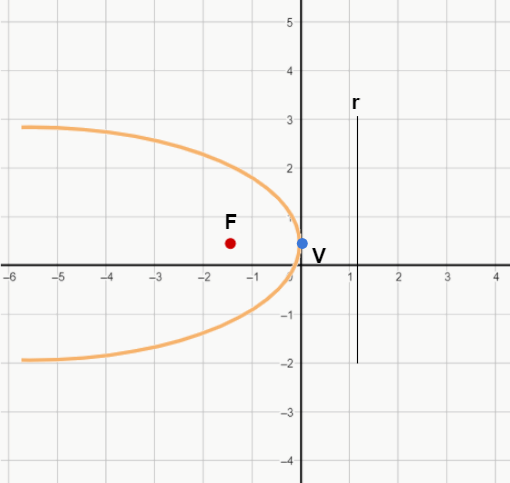
Nessas equações, p é distância do foco à reta diretriz e x e y são quaisquer coordenadas da figura.
Dadas todas as condições necessárias para construir uma parábola, parece ser bem difícil desenhá-la corretamente sem a utilização de softwares, né? Mas sabia que é possível construí-la utilizando um esquadro, um giz e um barbante? Assista o vídeo a seguir.
E é isso, finalizamos aqui o nosso assunto sobre cônicas. Você deve ter percebido que não falamos sobre a circunferência, mas isso aconteceu pois há um módulo inteirinho só para ela. Vá lá conferir 😉