Estudo da Circunferência

Podemos definir uma circunferência como um conjunto de pontos que possuem a mesma distância (são equidistantes) de um ponto central C (conhecido como “centro da circunferência”). Assim como a elipse, a hipérbole, e a parábola, a circunferência também é uma figura cônica e, portanto, pode ser obtida através de um corte paralelo à base do chamado cone duplo de revolução.

Selecione aqui o conteúdo que deseja ver!

Equação da circunferência

Posição entre circunferência e ponto

Posição entre circunferência e reta

Posição entre circunferências

Posição relativa entre circunferência e ponto

Saber calcular a distância entre dois pontos é uma habilidade importante e que pode nos oferecer algumas informações bem úteis. Por exemplo, como saber se um ponto está na parte interna, externa ou mesmo faz parte da circunferência? Para isso, temos que utilizar a fórmula da distância entre dois pontos, e como estamos falando da circunferência, um desses pontos será o centro da figura, e o outro, um ponto de interesse qualquer. Desse modo, o cálculo é feito a partir da fórmula a seguir:

\[ d = \sqrt{(xb – xa)^{2} + (yb – ya)^{2}} \]

Onde x_a e y_a são as coordenadas do centro da circunferência e x_be y_b são as coordenadas de um ponto qualquer.

Mas como saber onde está o ponto a partir deste cálculo? A fim de descobrir a posição relativa do ponto, temos que comparar o valor encontrado no cálculo da distância entre ponto e centro com o raio da figura. Vamos ver cada um dos casos.

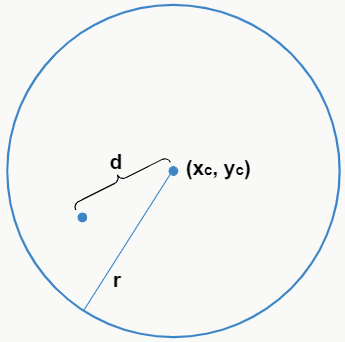
– Ponto interno à circunferência

Se a distância de um ponto qualquer ao centro da circunferência for menor que o raio dessa circunferência, ou seja, d < r, então o ponto encontra-se dentro da figura.

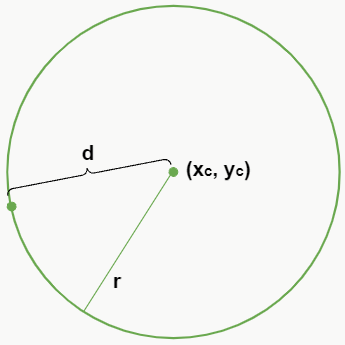
– Ponto pertence à circunferência

Se a distância de um ponto qualquer ao centro da circunferência for igual ao raio dessa circunferência, ou seja, d = r, então o ponto pertence à figura.

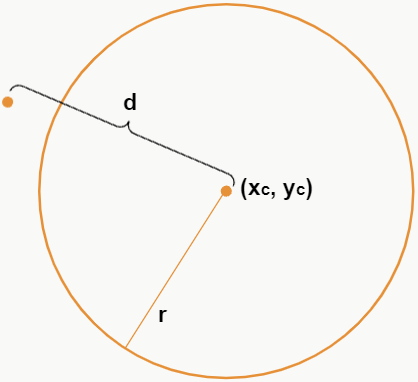
– Ponto externo à circunferência

Se a distância de um ponto qualquer ao centro da circunferência for maior que o raio dessa circunferência, ou seja, d > r,então o ponto encontra-se dentro da figura.

Exemplo: dada uma circunferência de equação reduzida (x + 6)² + (y – 3)² = 5², verifique qual é sua posição em relação ao ponto P = (4, 7).

Para começar, precisamos identificar qual é o centro da circunferência olhando para a equação reduzida. Fazendo isso, vemos que o centro está C = (-6, 3).

Sabendo disso, basta aplicarmos agora a fórmula da distância entre dois pontos.

\[ d = \sqrt{(4 + 6)^{2} + (7 – 3)^{2}} \] \[ d = \sqrt{10^{2} + 4^{2}} \] \[ d = \sqrt{100 + 16} = \sqrt{116}\] \[ d = 10,8 \]

Agora que descobrimos que a distância entre o centro e o ponto é 10,8, temos que comparar com o raio da circunferência. E onde encontramos essa informação? Exatamente, na equação reduzida!

Olhando novamente a equação reduzida, vemos que r = 5. Dessa forma, se a distância é 10,8, então temos que d > r, ou seja, o ponto está externo à circunferência. 🙂

Bem interessante, né? Mas ainda há outros elementos da geometria que podem nos oferecer informações bem importantes. Vamos ver mais sobre isso?

<– Equação da circunferência

Posição entre circun. e reta –>

Referências

Posições relativas entre ponto e circunferência

https://mundoeducacao.uol.com.br/matematica/posicao-relativa-entre-ponto-circunferencia.htm

https://brasilescola.uol.com.br/matematica/posicoes-relativas-entre-um-ponto-uma-circunferencia.htm

Distância entre dois pontos

https://brasilescola.uol.com.br/matematica/distancia-entre-dois-pontos.htm