Estudo da Circunferência
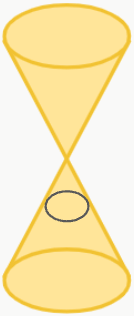
Podemos definir uma circunferência como um conjunto de pontos que possuem a mesma distância (são equidistantes) de um ponto central C (conhecido como “centro da circunferência”). Assim como a elipse, a hipérbole, e a parábola, a circunferência também é uma figura cônica e, portanto, pode ser obtida através de um corte paralelo à base do chamado cone duplo de revolução.
Selecione aqui o conteúdo que deseja ver!
Posição relativa entre circunferência e reta
Quando falamos sobre a posição relativa entre uma reta e a circunferência, o que estamos fazendo é verificar quantos pontos em comum essas figuras possuem. E para descobrir essa quantidade de pontos em comum, precisamos utilizar a equação geral da reta e a fórmula da distância entre ponto e reta.
Onde a, b e c são, respectivamente, os índices de x, y e do termo independente na equação da reta, e xc e yc são as coordenadas do centro da circunferência.
Desse modo, calculando a distância entre reta e circunferência, podemos encontrar as seguintes posições relativas.
– Reta secante à circunferência
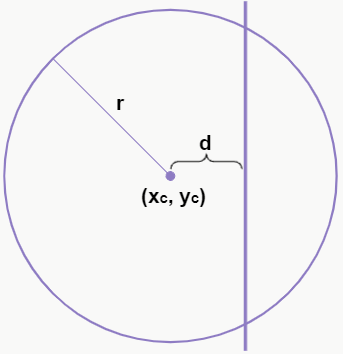
Se a distância entre a reta e o centro da circunferência é menor que o raio, ou seja, d < r, então as figuras possuem dois pontos em comum, pois a reta “corta” a circunferência.
– Reta tangente à circunferência
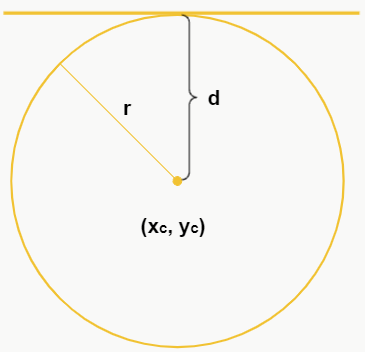
Se a distância entre a reta e o centro da circunferência é igual ao raio, ou seja, d = r, então as figuras possuem apenas um ponto em comum, pois a reta apenas “encosta” na circunferência.
– Reta externa à circunferência
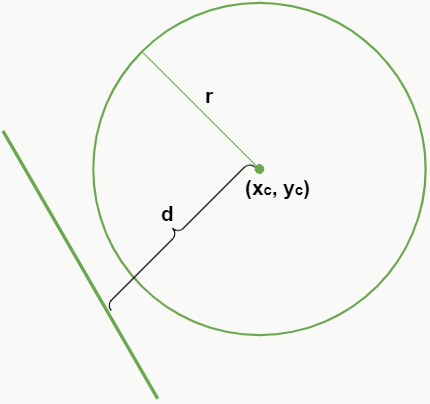
Se a distância entre a reta e o centro da circunferência é maior que o raio, ou seja, d > r, então as figuras não possuem pontos em comum, pois a reta está totalmente fora da circunferência.
Exemplo: dada a circunferência de equação reduzida (x + 1)2 + (y + 1)2 = 42 e a reta de equação geral 6x – 3y + 2 = 0, calcule a posição relativa entre as figuras.
Primeiramente, temos que identificar as coordenadas do centro da circunferência através da equação reduzida. Fazendo isso, encontramos que C = (-1, -1).
Também precisamos identificar os índices a, b e c da equação da reta. Desse modo, temos que a = 6, b = -3 e c = 2.
Com todas essas informações em mãos, basta aplicar a fórmula da distância entre ponto e reta.
Tirando o módulo da equação e resolvendo a raiz, temos que:
Por fim, sabendo que a distância é 0,15, temos que comparar com o raio da circunferência, que, de acordo com a equação reduzida, é r = 4. Dessa maneira, como a distância é menor que o raio, ou seja, r < d, então a reta está secante à circunferência. 🙂
Tranquilo, né? Para finalizar o assunto, vamos dar uma olhada no que acontece quando temos duas circunferências no plano!
Referências
Posições relativas entre circunferência e reta
https://mundoeducacao.uol.com.br/matematica/posicao-relativa-entre-uma-reta-uma-circunferencia.htm
https://www.preparaenem.com/matematica/posicao-relativa-entre-uma-reta-uma-circunferencia.htm