Estudo da Circunferência

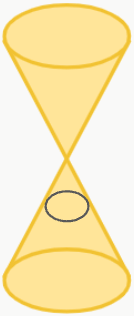
Podemos definir uma circunferência como um conjunto de pontos que possuem a mesma distância (são equidistantes) de um ponto central C (conhecido como “centro da circunferência”). Assim como a elipse, a hipérbole, e a parábola, a circunferência também é uma figura cônica e, portanto, pode ser obtida através de um corte paralelo à base do chamado cone duplo de revolução.

Posição relativa entre circunferências

Quando temos duas circunferências no plano, também podemos fazer a análise da posição relativa entre elas. Para isso, precisamos conhecer a medida de seus raios e as posições de seus centros, que podemos encontrar a partir da equação da circunferência.

(x – x_c)² + (y – y_c)² = r²

Onde x e y são as coordenadas de um ponto qualquer da circunferência, x_c e y_c são as coordenadas do centro, e r é o raio.

Sabendo dos valores do centro, precisamos utilizar a fórmula da distância entre dois pontos (os centros) para descobrir a posição relativa entre elas.

Onde x_a e y_a são as coordenadas do centro da circunferência e x_b e y_b são as coordenadas de um ponto qualquer.

Sendo assim, vamos ver quais são as possíveis posições relativas entre duas circunferências.

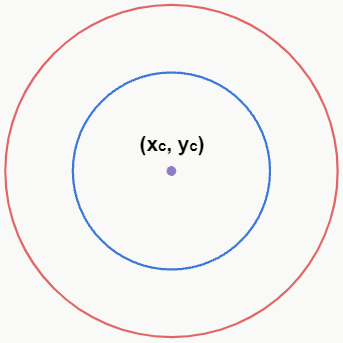
– Concêntricas

Se a distância entre os centros for igual a 0, ou seja, se d = 0, isso significa que ambas as circunferências possuem o mesmo centro.

– Internas

Se a distância entre os centros for menor que a diferença entre os raios das circunferências, ou seja, d < r1 – r2, então uma circunferência está dentro da outra, e elas não possuem pontos em comum.

– Tangente interna

Se a distância entre os centros for igual a diferença entre os raios das circunferências, ou seja, d = r1 – r2, então uma circunferência está dentro da outra, e elas possuem um ponto em comum.

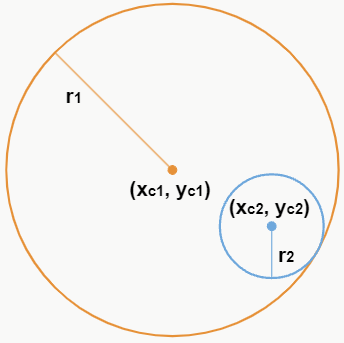
– Coincidentes

Se duas circunferências possuem o mesmo centro (C1 = C2) e o mesmo raio (r1 = r2), isso significa que elas ocupam exatamente o mesmo espaço no plano, pois uma está “sobre” a outra.

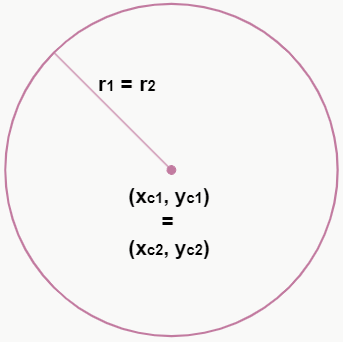
– Secante

Se a distância entre os centros for maior que a diferença entre os raios das circunferências e menor que a soma dos dois raios, ou seja, r1 – r2 < d < r1 + r2, então as circunferências possuem dois pontos em comum.

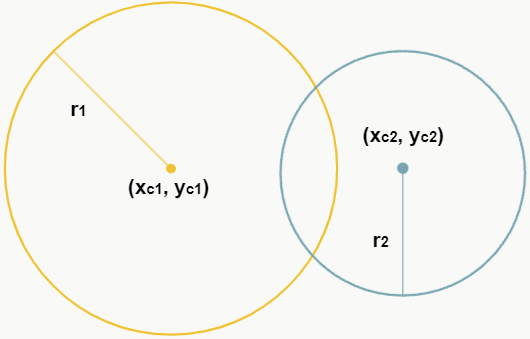
– Tangente externa

Se a distância entre os centros for igual a soma entre os raios das circunferências, ou seja, d = r1 + r2, isso significa que uma circunferência está externa à outra, porém, elas possuem um ponto em comum.

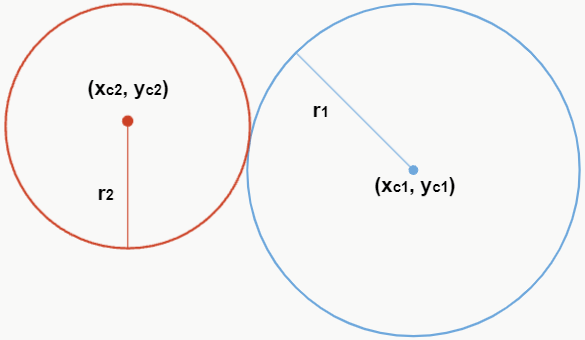
– Externas

Se a distância entre os centros for igual a soma entre os raios das circunferências, ou seja, d > r1 + r2, isso significa que uma circunferência está externa à outra e não possuem pontos em comum.

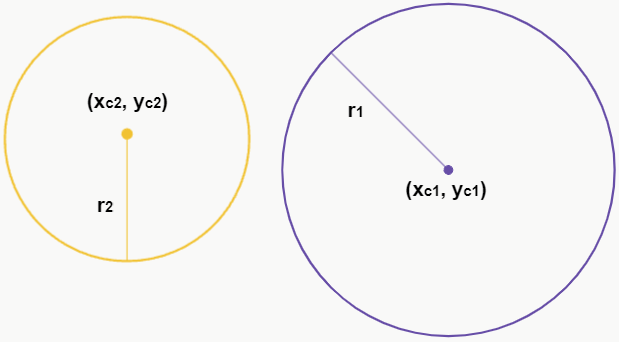
Exemplo: dadas as circunferências de equações reduzidas A: (x – 2)² + (y – 4)² = 8² e B: (x + 5)² + (y – 3)² = 6², encontre a posição relativa entre elas.

Para encontrar o que pede o exemplo, precisamos primeiramente encontrar as coordenadas dos centros das circunferências. Desse modo, C_A = (2, 4) e C_B = (-5, 3). 

Sabendo disso, temos que calcular a distância entre esses centros utilizando a fórmula da distância entre dois pontos.

Sabendo que a distância entre os centros é 7,07, precisamos agora comparar com os raios das figuras, que, pelas equações reduzidas, são, r₁ = 8 e r₂ = 6. E como a distância está entre os valores dos raios, ou seja, r₂ < d < r₁, então a posição relativa entre as circunferências é secante. 🙂

E é isso, finalizamos aqui o estudo da circunferência. Todas as informações vistas ao longo das páginas nos mostram o quão conectadas estão as várias partes da geometria analítica, e como a partir de uma figura conseguimos encontrar informações sobre outras.

Referências

Posições relativas entre circunferências

https://mundoeducacao.uol.com.br/matematica/posicao-relativa-entre-duas-circunferencias.htm

https://brasilescola.uol.com.br/matematica/circunferencia-posicoes-relativas.htm

https://www.infoescola.com/matematica/posicoes-relativas-entre-duas-circunferencias/