Estudo do Ponto e Reta

O estudo do ponto e da reta é fundamental para a geometria, pois esses elementos constituem a base de toda a disciplina. Além disso, podemos utilizá-los para descobrir informações importantes sobre diversas figuras geométricas, como a circunferência, por exemplo.

Posições relativas entre retas

Quando estão em diferentes planos, duas ou mais retas são chamadas de reversas, porém quando estão em um mesmo plano, elas são chamadas de coplanares e podem estar em diferentes posições. Vamos dar uma olhada em cada uma delas.

– Retas coincidentes

Duas ou mais retas são ditas coincidentes quando fazem parte do mesmo plano e possuem todos os pontos em comum.

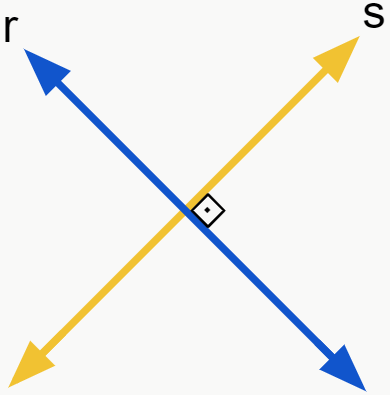
– Retas concorrentes

Duas ou mais retas são ditas concorrentes quando elas possuem um ponto em comum, ou seja, quando se cruzam.

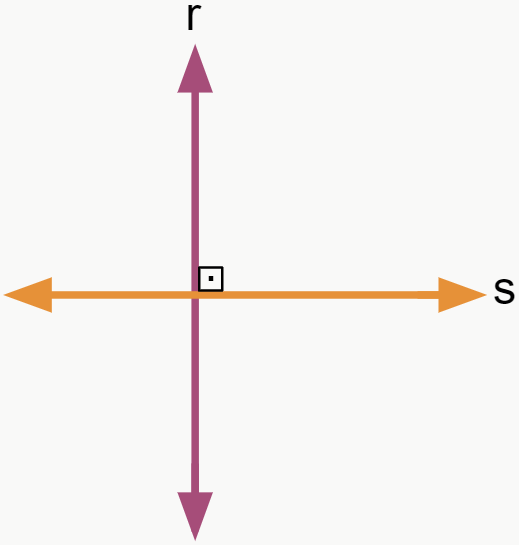
– Retas perpendiculares

Quando retas concorrentes formam um ângulo de 90° entre si, dizemos que elas são perpendiculares.

– Retas paralelas

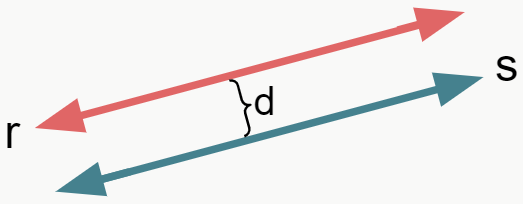
Duas ou mais retas são paralelas quando elas não possuem nenhum ponto em comum. Nesse caso, a distância entre seus pontos é a mesma para toda a reta.

O Teorema de Tales

Sabendo que duas ou mais retas são paralelas, podemos utilizar o Teorema de Tales para realizar alguns cálculos importantes. Mas o que diz este teorema?

Ele diz que “a intersecção de um feixe de retas paralelas por duas retas transversais formam segmentos proporcionais”. Traduzindo… Isso quer dizer que, se temos duas ou mais retas paralelas que são “cortadas” por outras retas (chamadas de transversais), as medidas de cada segmento (divididos pelas retas paralelas) das retas transversais são proporcionais entre si. Veja a figura a seguir:

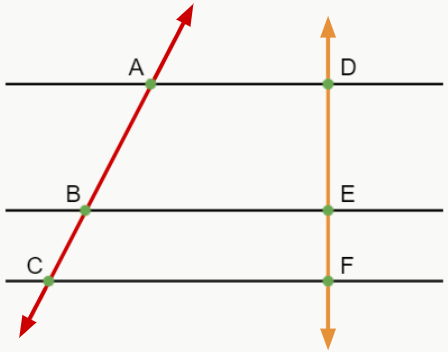
Note que as retas paralelas deram origem aos segmentos AB e BC (reta vermelha) e DE e EF (reta amarela). Desse modo, de acordo com o teorema, a medida desses segmentos são proporcionais aos segmentos correspondentes (que estão entre as mesmas retas paralelas) da outra reta. Podemos então estabelecer a seguinte relação:

Ou seja, a razão entre AB e BC é igual à razão entre DE e EF. Portanto, os segmentos são proporcionais.

Para finalizar o módulo, vamos calcular algumas distâncias?

Referências