Poliedros
Poliedros são figuras tridimensionais formadas por diversos polígonos. Não é difícil encontrar poliedros por aí, dê uma olhada rápida ao seu redor e você com certeza irá encontrar vários. Se não encontrou, é porque talvez não saiba de fato o que são essas figuras tão interessantes. Então que tal aprender sobre elas?
Selecione aqui o conteúdo que deseja ver!
Pirâmides
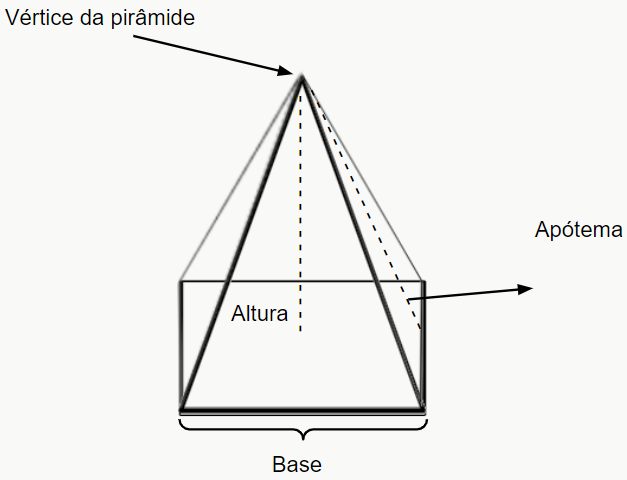
Pirâmides são figuras espaciais que possuem uma base formada por um polígono qualquer e lados triangulares. O ponto mais alto da pirâmide, que é onde todos os triângulos laterais se encontram, é chamado de vértice da pirâmide. Os outros vértices, os da base, são só vértices mesmo, sem nenhum nome especial.
Além do vértice da pirâmide, há outros elementos importantes que fazem parte desta figura:
- Base: região de sustentação da pirâmide.
- Altura: distância da base até o vértice da pirâmide.
- Apótema: corresponde à altura dos triângulos que formam as faces laterais.
Tipos de pirâmides
Assim como os prismas, o tipo da pirâmide dependerá do polígono que forma sua base. Desse modo, podemos classificá-las como:
- Triangular: base formada por triângulo (3 lados).
- Quadrangular: base formada por quadrado (4 lados).
- Pentagonal: base formada por pentágono (5 lados).
- Hexagonal: base formada por hexágono (6 lados).
- …
E assim por diante. Além disso, a figura da base irá influenciar a maneira como calculamos a área e o volume da pirâmide. Vamos ver agora como realizar esses cálculos.
Área da pirâmide
Como depende do tipo de base, a fórmula geral para o cálculo de área dessas figuras é:
A = Ab + Al
Onde Ab é a área da base e Al é a área lateral (constituída pela soma da área de todos os triângulos que formam a pirâmide).
Exemplo: calcule a área de uma pirâmide quadrangular com aresta da base 5 cm e altura 10 cm.
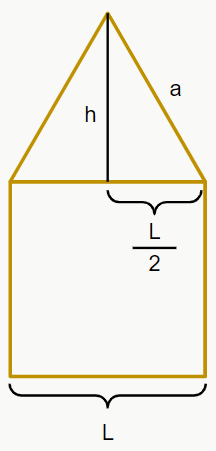
Para calcular a área de uma pirâmide, precisamos saber qual o valor da apótema que formam os triângulos das faces. Aqui não temos o valor da apótema (a), mas sabemos a medida da aresta da base (L) e a altura (h), o que nos permite calcular a apótema através do Teorema de Pitágoras.
Perceba que utilizamos L/2. Isso acontece pois a base do triângulo retângulo corresponde a metade do valor da aresta da base da pirâmide.
Seguindo:
Agora que sabemos quanto vale a apótema do triângulo, podemos calcular a área da pirâmide quadrangular.
Mas essa é a área de apenas 1 triângulo. Como são quatro triângulos formando os lados, temos que multiplicar por 4.
Por fim, temos que somar os valores encontrados.
Volume da pirâmide
O volume da pirâmide vai na mesma direção da área, porém, agora só precisamos saber da área da base e da altura da pirâmide. Dessa forma, a fórmula para calcular o volume de uma pirâmide qualquer é:
Onde Ab é a área da base e h é a altura da pirâmide.
Exemplo: calcule o volume de uma pirâmide triangular com aresta da base de 3 cm e altura 12 cm.
Como temos tudo que precisamos, basta calcular a área da base (área do triângulo equilátero) e aplicar a fórmula do volume.
Para finalizar o assunto, vamos ver onde encontrar essas formas.
E aqui terminamos nosso módulo sobre poliedros!


