Poliedros
Poliedros são figuras tridimensionais formadas por diversos polígonos. Não é difícil encontrar poliedros por aí, dê uma olhada rápida ao seu redor e você com certeza irá encontrar vários. Se não encontrou, é porque talvez não saiba de fato o que são essas figuras tão interessantes. Então que tal aprender sobre elas?
Selecione aqui o conteúdo que deseja ver!
Conceitos
Tipos de poliedros
– Convexos
Observe a imagem a seguir:
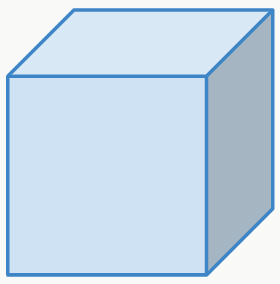
Agora vamos pegar uma reta, formada pelos pontos A e B, e colocá-la de modo que os pontos fiquem dentro da figura.
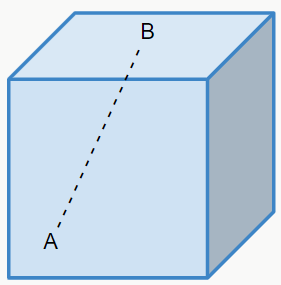
Perceba que a reta está totalmente dentro da figura (linha pontilhada). Quando isso acontece, dizemos que o poliedro é convexo. Mas e se isso não acontecer?
– Não Convexos
Se o caso acima não ocorrer, dizemos que o poliedro é não convexo. Vamos dar uma olhada na imagem a seguir, executando o mesmo procedimento feito no caso anterior:
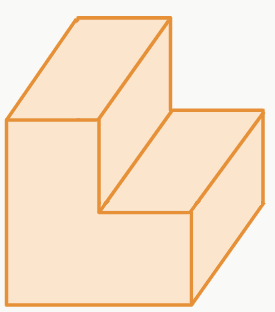
Agora vamos colocar a mesma reta AB dentro da figura.
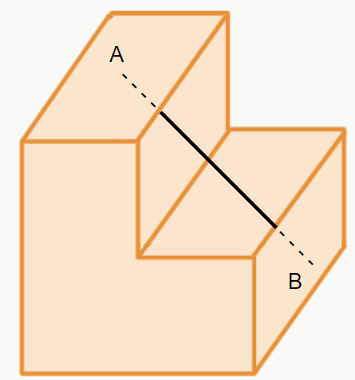
Olha só o que aconteceu desta vez. Uma parte da reta (formada pela linha sólida) está fora da figura. Desse modo, a figura não pode ser convexa, e portanto, é não convexa.
Mas como construir um poliedro?
Elementos de um poliedro
- Faces: superfícies representadas pelos polígonos que formam o poliedro.
- Arestas: são os segmentos de reta que formam os lados do poliedro.
- Vértices: consistem nos pontos de encontro (intersecção) de duas arestas.
Os elementos acima estão ilustrados na figura a seguir:
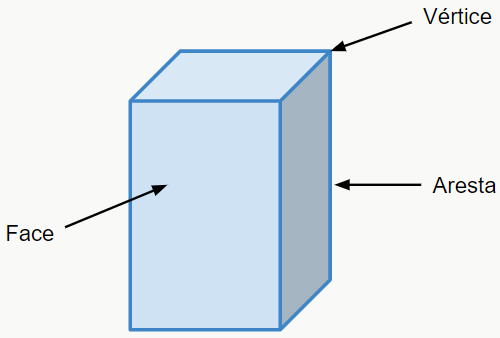
Sabendo disso, agora podemos ver mais um tipo de poliedro.
– Poliedros regulares
Para que um poliedro seja regular, ele deve respeitar algumas condições: 1) Deve ser convexo, 2) Deve ser formado por polígonos regulares (figuras que possuem ângulos e lados com mesma medida).
Mas quem são eles?
Existem apenas cinco deste tipo de poliedros, sendo eles:
- Tetraedro: figura formada por 4 vértices, 4 faces triangulares e 6 arestas.
- Hexaedro: figura formada por 8 vértices, 6 faces quadrangulares e 12 arestas.
- Octaedro: figura formada por 6 vértices, 8 faces triangulares e 12 arestas.
- Dodecaedro: figura formada por 20 vértices, 12 faces pentagonais e 30 arestas.
- Icosaedro: figura formada por 12 vértices, 20 faces triangulares e 30 arestas.
Mas há alguma relação entre a quantidade de vértices, arestas e faces de um poliedro? Tem sim, e é isso que veremos agora.
Relação de Euler
A Relação de Euler é uma expressão que nos permite relacionar os vértices, arestas e faces de um poliedro. Ela é válida para todos os poliedros convexos e para alguns não convexos. A expressão é a seguinte:
V – A + F = 2
Sendo V os vértices, A as arestas e F as faces do poliedro.
Essa expressão pode nos ajudar a encontrar a quantidade de um dos elementos da figura. Vamos testar a fórmula com uma figura que já conhecemos bem, os tetraedros, que como mostrado anteriormente, possuem 8 vértices, 6 faces quadrangulares e 12 arestas. A equação nos diz que a soma dos elementos deve ser igual a 2, então se substituirmos os valores na expressão, temos que chegar a dois, certo? Então vamos lá.
8 – 12 + 6 = 2
-4 + 6 = 2
2 = 2
Olha só, deu certo! Se você testar outros poliedros convexos já conhecidos, vai que ela funciona também.
Agora que já vimos todos os conceitos, vamos focar nos poliedros mais importantes e descobrir algumas coisas interessantes sobre eles.