Poliedros
Poliedros são figuras tridimensionais formadas por diversos polígonos. Não é difícil encontrar poliedros por aí, dê uma olhada rápida ao seu redor e você com certeza irá encontrar vários. Se não encontrou, é porque talvez não saiba de fato o que são essas figuras tão interessantes. Então que tal aprender sobre elas?
Selecione aqui o conteúdo que deseja ver!
Prismas
Prismas são figuras espaciais que possuem duas bases paralelas, além de faces laterais planas. Os prismas possuem algumas classificações e diversos tipos, que dependem da figura que forma sua base. Lembra do cubo e do paralelepípedo vistos na página anterior? Veja que eles se encaixam perfeitamente na definição de prismas. E isso acontece porque eles são, na verdade, prismas!
Classificação dos prismas
– Prisma reto
É um prisma que possui arestas laterais totalmente na vertical. De modo mais formal, é um sólido que possui arestas laterais ortogonais (que formam ângulos de 90°) à base. Os lados são retângulos. Exemplo:
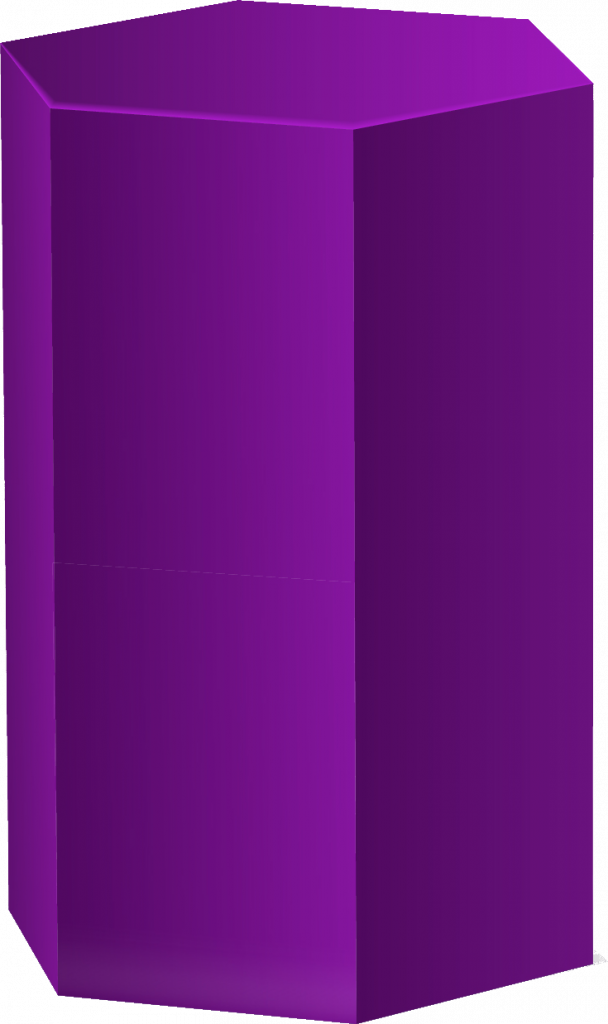
– Prisma oblíquo
É um prisma que possui arestas laterais inclinadas. Em outras palavras, é um sólido que possui arestas laterais não ortogonais à base. Os lados são paralelogramos. Exemplo:

Agora que já sabemos como classificá-los, vamos dar uma olhada nos tipos existentes.
Tipos de prismas
O tipo do prisma vai depender do polígono que forma suas bases. Desse modo, um prisma pode ser:
- Triangular: base formada por triângulo (3 lados).
- Quadrangular: base formada por quadrado (4 lados).
- Pentagonal: base formada por pentágono (5 lados).
- Hexagonal: base formada por hexágono (6 lados).
- Heptagonal: base formada por heptágono (7 lados).
- Octogonal: base formada por octógono (8 lados).
- Eneagonal: base formada por eneágono (9 lados).
- Decagonal: base formada por decágono (10 lados).
- …
E assim por diante. Outra coisa que vai depender da base do prisma é o modo como calculamos a área e o volume. Isso porque cada polígono possui uma área diferente, então é necessário analisar qual é a base para seguir com as contas.
Área do prisma reto
Calcular a área de um prisma é simplesmente somar a área lateral com a área da base. Contudo, isso vai depender do tipo de prisma reto, então a fórmula mais genérica que temos para esse tipo de figura é:
A = 2Ab + Al
Onde Ab é a área da base e Al é a área lateral (constituída pela soma da área de todos os retângulos que formam o prisma). Exemplo: calcule a área do seguinte prisma.
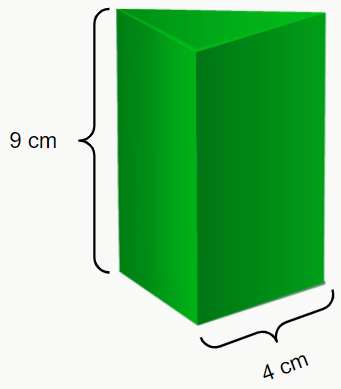
Vamos analisar a figura. O sólido é um prisma de base triangular e com faces laterais compostas por retângulos. Então o cálculo é bem simples, né? É só calcular as áreas dessas figuras.
Al = 4 * 9 = 36 cm2 → 36 * 3 = 108 cm2
Como são 3 retângulos, fizemos 36 * 3.
Agora podemos voltar para a fórmula inicial e obter a área total:
Volume do prisma reto
O mesmo vale para o volume, tudo vai depender da figura que forma a base. Desse modo, a fórmula para o volume de um prisma reto é:
V = Ab * h
Sendo Ab a área da base e h a altura do prisma. Exemplo: calcule o volume do seguinte prisma.
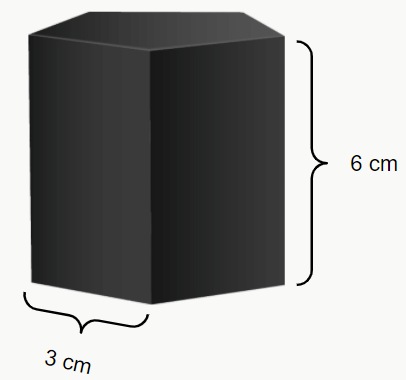
Primeiramente temos que analisar a figura. É um prisma pentagonal, então para calcular o volume, precisamos calcular a área desse pentágono. E como calculamos essa área?
Você pode utilizar a fórmula da área do pentágono: A = 5L * a, onde a é a apótema (altura) dos triângulos que formam a figura. Porém, não sabemos qual o valor dessa apótema, então o que podemos fazer? Se você disse trigonometria, acertou.
Na página sobre polígonos, falamos sobre como podemos calcular os ângulos internos de cada figura, e é isso que faremos agora. Um pentágono possui ângulo interno total de 540°. Ao dividir por 5, vemos que cada lado possui 108°. Observe a figura a seguir:
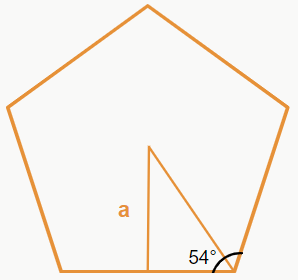
Perceba que é possível colocar um triângulo retângulo, e a altura desse triângulo é justamente a apótema. Como vimos, cada lado do pentágono possui um ângulo de 108°, então ao dividir esse ângulo em dois para colocar o triângulo, fica claro que agora temos dois ângulos de 54°.
Queremos descobrir a altura do triângulo, que corresponde ao cateto oposto ao ângulo de 54°. Desse modo, como temos o valor do cateto adjacente (1,5 cm), basta utilizar a tangente de 54°, que é aproximadamente 1,38.
Portanto, a apótema é igual a 2,07 cm. Sabendo disso, podemos voltar para a fórmula da área do pentágono.
A = 5 * 3 * 2,07 = 31,05 cm2
Detalhe importante! Esse mesmo processo (utilizando trigonometria), pode ser feito para qualquer polígono regular. Desse modo, fica fácil de calcular a apótema da base sempre que necessário.
Agora que encontramos a área, basta multiplicá-la pela altura para encontrar o volume do prisma.
V = 31,05 * 6
V = 186,30 cm3
E lá vamos nós para a última figura desse módulo sobre poliedros. Vamos falar sobre pirâmides!
Atribuições
Prismas: Geometric vector created by macrovector – www.freepik.com