Circunferência e Círculo
Circunferências e círculos são figuras planas bem comuns no cotidiano. Quem nunca viu um bambolê, um anel, um relógio ou uma roda de bicicleta? Desse modo, é importante saber como diferenciá-las e como calcular algumas informações importantes, como área, perímetro, comprimento de arcos, além de entender como utilizar os ângulos presentes no círculo. É… esse assunto tem mais coisas do que você pensou, né? Vamos estudá-lo então?
Selecione aqui o conteúdo que deseja ver!
Ângulos côngruos e expressões trigonométricas
Até agora falamos que uma volta completa na circunferência trigonometria equivale a 360°. Porém, será que é possível superar esses 360°? A resposta é: sim, basta dar mais de uma volta na circunferência. Por exemplo, em uma volta e meia temos 360° + 180° = 540°, concorda?
Mas e agora? Como é que vou saber o valor das relações desses ângulos? Na verdade você já sabe, mas falta introduzir um conceito para que você tenha certeza disso. Esse conceito é o que chamamos de ângulos côngruos.
Os ângulos côngruos são ângulos que possuem valores diferentes, mas que estão em um mesmo ponto da circunferência. Por exemplo, 540° está na mesma posição que 180°. Por quê? Pois se fizermos a divisão inteira 540/360, teremos como resto 180, o que nos indica que o ângulo 540° ocupa a mesma posição de 180°. Veja as figuras a seguir:
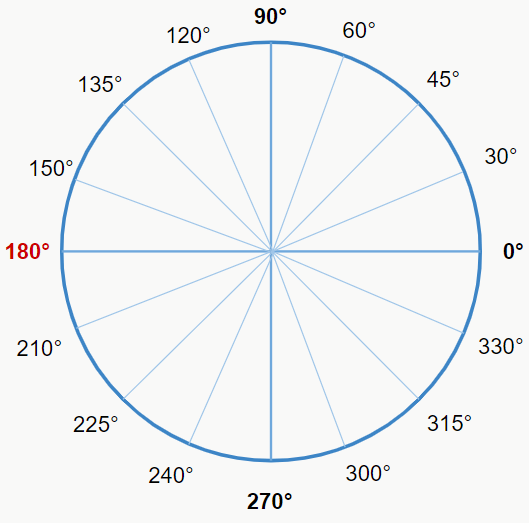
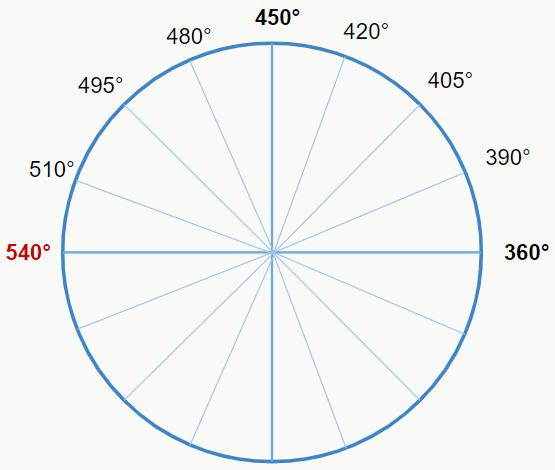
Viu como funciona? Os ângulos estão na mesma posição, porém, o 180° é encontrado após meia volta, enquanto o 540° é encontrado após uma volta e meia. Então é essa a regra que você deve seguir para saber se dois ângulos são côngruos ou não. Vamos ver uns exemplos:
Ex. 1: 750° é côngruo de 60°? Vamos verificar:
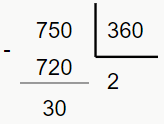
Logo, 750° é côngruo de 30°, e não de 60°.
Ex. 2: 810° é côngruo de 90°? Vamos verificar:
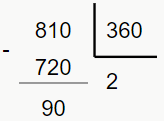
Logo, 810° é côngruo de 90°.
Mas por que isso é importante? Pode ser que precisamos saber o valor de algum ângulo maior que 360° em algum momento, e com essa técnica agora já podemos encontrar esse valor tranquilamente. Quer um exemplo?
Vai que em algum momento você tenha que resolver uma equação do tipo:
x = sen(750°) + sen(450°)
A resolução é simples, basta substituir esses valores, mas para isso temos que descobrir onde estão 750° e 450° na circunferência. Vamos então realizar o procedimento já visto:
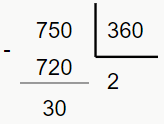
Seguindo:
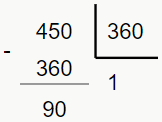
Logo, 450° é côngruo de 90°, então sen(450°) = sen(90°) = 1.
Substituindo na equação:
E é isso, quando você se deparar com uma expressão desse tipo, onde basta substituir os valores das relações, pode ser que precise encontrar os ângulos côngruos a fim de facilitar seus cálculos.
FIM! Esse foi nosso módulo sobre circunferência e círculo.