Triângulos

Não há dúvidas de que o triângulo é uma das figuras mais importantes da geometria (talvez até a mais importante). Mas por quê? Se você viu a página sobre polígonos, viu que podemos dividir alguns dos polígonos regulares em diversos triângulos, ou seja, com apenas uma figura podemos resolver diversos tipos de problemas, o que facilita muito a nossa vida. 

Já que essas figuras são tão importantes assim, que tal conhecer mais sobre elas?

Área do triângulo

Os triângulos, assim como as outras figuras planas, possuem área. Já sabemos que existem diversos tipos de triângulos, mas como calculamos a área de cada um deles?

– Triângulo retângulo

Como sabemos, um triângulo retângulo é aquele que possui um ângulo de 90°. Desse modo, o cálculo da área desta figura segue a seguinte equação:

Sendo b a medida da base do triângulo e h a altura do triângulo. Conforme a figura a seguir:

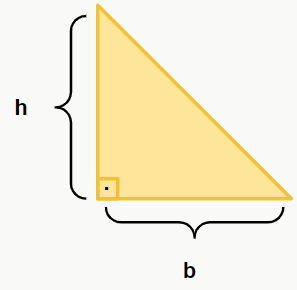
Mas e se não soubermos a altura do triângulo? Aí basta utilizar o Teorema de Pitágoras visto anteriormente para encontrar este valor. 😉

– Triângulo isósceles

Um triângulo isósceles é aquele possui dois lados com mesma medida. Então como encontramos sua área? Exatamente da mesma forma que fizemos para o triângulo retângulo, utilizando a equação:

Sendo b a medida da base do triângulo e h a altura do triângulo. Conforme a figura a seguir:

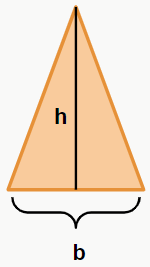
E como encontramos a altura? Basta utilizar o Teorema de Pitágoras. Perceba que a altura (h) do triângulo isósceles divide a figura em dois triângulos retângulos, e isso nos permite utilizar o Teorema.

– Triângulo equilátero

Um triângulo equilátero é aquele que possui todos os lados com a mesma medida. Mas encontrar sua área? Olha só que surpresa, utilizamos a fórmula:

Sendo b a medida da base do triângulo e h a altura do triângulo. Conforme a figura a seguir: 

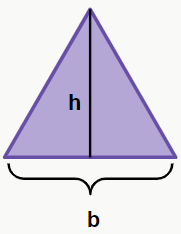
Mas temos um porém aqui. Nos outros casos, se não sabemos a altura, podemos utilizar o Teorema de Pitágoras para encontrá-la, e aqui também podemos fazer isso, mas não é necessário. Vamos ver por quê?

Primeiramente temos que dividir o triângulo equilátero em dois triângulos retângulos, conforme a figura a seguir:

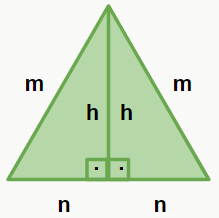
Agora já estamos aptos a aplicar o Teorema. Na figura anterior, temos os lados m (hipotenusa), n (cateto) e h (cateto). Substituindo na fórmula do Teorema:

Porém, como estamos falando de um triângulo equilátero, isso significa que todos os lados possuem a mesma medida, não é? Logo, temos que n = m/2. Substituindo na equação anterior:

Isolando h, temos que:

Lembra da fórmula inicial? 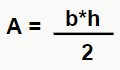. Agora que sabemos o valor de h, podemos substituí-lo nessa equação:

Ou seja, a área de um triângulo equilátero não depende da sua altura, mas somente da medida dos lados, o que torna tudo bem mais fácil. Veja que não é necessário decorar essa fórmula, pois ela pode ser facilmente obtida a partir da junção da equação inicial com o valor de h encontrado no Teorema de Pitágoras.

– Triângulo escaleno

Um triângulo escaleno é aquele que possui todos os lados e ângulos com medidas diferentes. Para encontrar a área desta figura, também partimos da fórmula 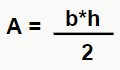, porém, como seus lados são todos diferentes, não temos como dividir o triângulo em duas partes iguais. Desse modo, iremos precisar da ajuda da trigonometria, que veremos com mais detalhes na próxima página. Como calcular a área então? Há três fórmulas diferentes, mas todas chegam na mesma resposta:

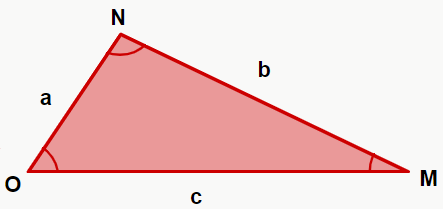
Sendo a, b, c os lados do triângulo e M, N, O os ângulos, conforme figura a seguir:

Cálculo de área com determinantes

Suponha que te peçam para calcular a área de um triângulo, mas te forneçam apenas as coordenadas dessa figura no plano cartesiano. O que você faria? Desenharia o plano cartesiano e colocaria esse triângulo nas coordenadas descritas? É uma opção, mas isso pode levar algum tempo, e se você tiver com pressa, todo esse processo pode te atrasar um pouco.

Desse modo, podemos calcular a área deste triângulo de outra forma, sem ao menos saber como é o formato da figura. Basta utilizar determinantes. 🙂

Para esse cálculo, iremos utilizar a fórmula:

Onde |D| é o módulo do determinante formado pelas coordenadas do triângulo. Mas como encontrar esse determinante? Supondo um triângulo de lados A, B e C, só precisamos montar uma matriz 3×3 da seguinte forma:

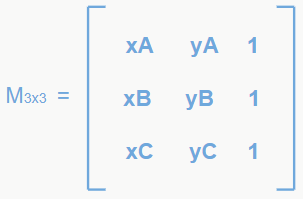
Ou seja, na coluna da esquerda vão as coordenadas x do triângulo, na do meio vão as coordenadas y, e na coluna da direita é só preencher todas as linhas com o número 1. Vamos fazer um exemplo para ficar mais claro?

Exemplo: calcule a área de um triângulo de vértices A = (4, 2), B = (4, 7), C = (9, 7).

Como temos as coordenadas do triângulo, a área será o determinante da matriz formada pelos vértices:

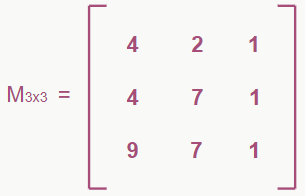
Resolvendo o determinante:

4(7*1-1*7) – 2(4*1-1*9) + 1(4*7-7*9) =

4*0 – 2*(-5) + 1*(-35) =

0 + 10 – 35 = -25

Mas como a área é dada pela metade do módulo do determinante, então temos que:

A = 12,5

Só para você ver que daria na mesma desenhar o triângulo, vamos resolver utilizando a fórmula 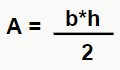que já vimos anteriormente.

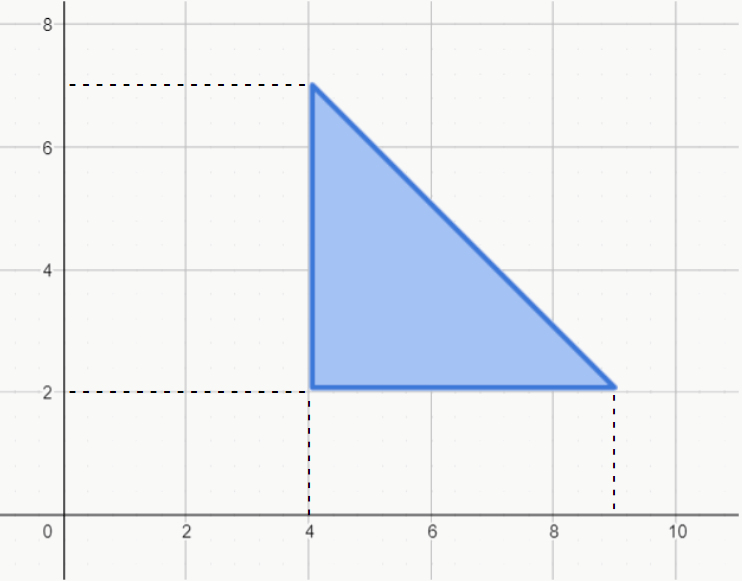
Como vemos na figura, a altura do triângulo será dada pela medida do lado paralelo ao eixo y, ou seja, 7-2 = 5. Já a base do triângulo será o lado paralelo ao eixo x, ou seja, 9-4 = 5.

Substituindo esses valores na fórmula, temos que:

A = 12,5

Que é o mesmo resultado encontrado com o cálculo do determinante da matriz 3×3. Por fim, para terminar esse assunto tão interessante que são os triângulos, vamos falar um pouco sobre trigonometria!

Referências

Área dos triângulos

https://www.todamateria.com.br/area-do-triangulo/

Área dos triângulos por determinantes

https://mundoeducacao.uol.com.br/matematica/area-triangulo-2.htm