Triângulos
Não há dúvidas de que o triângulo é uma das figuras mais importantes da geometria (talvez até a mais importante). Mas por quê? Se você viu a página sobre polígonos, viu que podemos dividir alguns dos polígonos regulares em diversos triângulos, ou seja, com apenas uma figura podemos resolver diversos tipos de problemas, o que facilita muito a nossa vida.
Já que essas figuras são tão importantes assim, que tal conhecer mais sobre elas?
Selecione aqui o conteúdo que deseja ver!
Conceitos
Tipos de triângulos
Existem vários tipos de triângulos, e podemos classificá-los conforme a medida dos seus lados e ângulos.
Classificação pela medida dos lados
Um triângulo é uma figura que possui 3 lados. Desse modo, podemos dividi-los em:
– Triângulo escaleno
É um triângulo que possui os três lados com tamanhos diferentes.
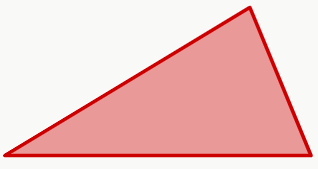
– Triângulo isósceles
É um triângulo que possui dois lados com o mesmo tamanho.
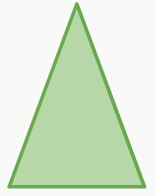
– Triângulo equilátero
É um triângulo que possui todos os lados com a mesma medida.
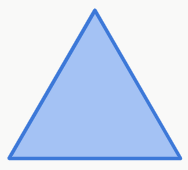
Legal, podemos classificar os triângulos de três formas diferentes. Mas será que basta ter três retas de qualquer tamanho para formarmos um triângulo?
A resposta é: não! Um triângulo é uma figura que segue uma condição de existência. É claro que deve ter três lados, mas devemos também atentar-nos para o tamanho desses lados, pois para que um triângulo exista, um lado deve ser obrigatoriamente menor que a soma dos outros dois e maior que o módulo da diferença dos outros lados. Dê uma olhada na figura a seguir:
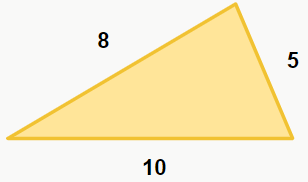
Perceba que é realmente um triângulo, e isso ocorre justamente porque seus lados seguem a condição de existência, que pode ser descrita pelas seguintes inequações:
| b – c | < a < b + c
| a – c | < b < a + c
| a – b | < c < a + b
Vamos testar as medidas do triângulo anterior para confirmar se é realmente um triângulo?
| 5 – 8 | < 10 < 8 + 5 = 3 < 10 < 13 → Correto
| 10 – 8 | < 5 < 10 + 8 = 2 < 5 < 18 → Correto
| 10 – 5 | < 8 < 10 + 5 = 5 < 8 < 15 → Correto
Portanto, a figura é realmente um triângulo. 🙂 Vamos imaginar agora um triângulo com as medidas A = 14, B = 3 e C = 5 e verificar se é possível construir um triângulo com elas.
| 3 – 5 | < 14 < 3 + 5 = 2 < 14 < 8 → Errado
| 14 – 5 | < 3 < 14 + 5 = 9 < 3 < 19 → Errado
| 14 – 3 | < 5 < 14 + 3 → 11 < 5 < 17 → Errado
Portanto, é impossível construir um triângulo com essas medidas. Neste caso, todas as condições deram errado, mas nem sempre isso acontece. Saiba que, se uma delas não der certo, a figura não pode ser um triângulo.
Classificação pela medida dos ângulos:
Em um triângulo, a medida dos ângulos internos é sempre 180°. Desse modo, podemos dividi-los em:
– Triângulo agudo (ou acutângulo)
É um triângulo que possui todos os ângulos menores que 90° (ângulo agudo).
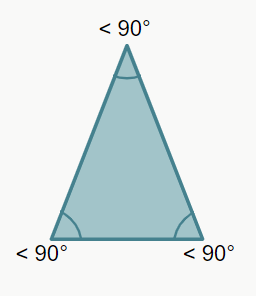
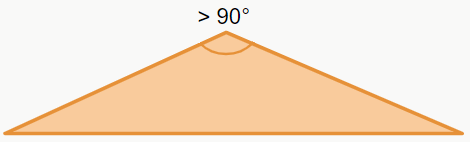
– Triângulo obtusângulo
É um triângulo que possui um ângulo maior que 90° (ângulo obtuso).
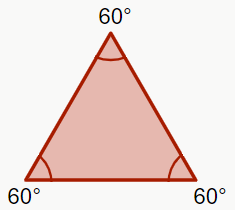
– Triângulo equiângulo
É um triângulo que possui todos os ângulos com a mesma medida. Como a soma dos ângulos internos é sempre 180°, cada ângulo será igual a 60°. Esse tipo de classificação ocorre apenas para triângulos equiláteros, pois eles possuem todos os lados com a mesma medida, e portanto, com mesma inclinação.
– Triângulo retângulo
É um triângulo que possui um ângulo de 90° (ângulo reto). Os lados deste triângulo recebem nomes especiais, sendo eles: cateto oposto, cateto adjacente e hipotenusa. O cateto oposto e o adjacente vão depender do ângulo agudo que tomamos como referência, porém, a hipotenusa é o lado oposto ao ângulo reto, e é conhecida por ser o maior lado de um triângulo retângulo. Vamos ver duas imagens para entendermos melhor:
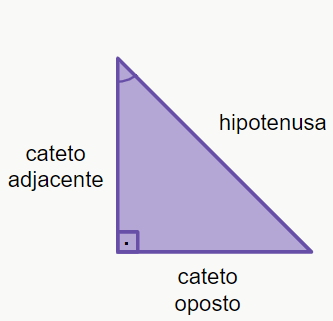
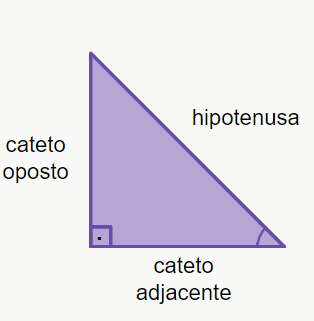
Perceba que, em ambas as figuras, a hipotenusa é o mesmo lado, porém, os catetos mudam de posição, pois tomamos como referência ângulo diferentes.
Agora que já sabemos como classificar os triângulos, vamos dar uma olhada em onde encontrá-los no dia a dia?
Legal né, os triângulos estão por toda parte. É claro que aqui foram mostrados alguns poucos exemplos, mas isso é o suficiente para que você já comece a perceber essas formas no seu cotidiano. Falando nisso, nas figuras 1 e 4 (que possuem estruturas), você consegue visualizar todos os tipos de triângulos existentes? Tente aí 😉
Para continuar o assunto, que tal darmos uma olhadinha em alguns cálculos?
Referências
Conceitos e classificação dos triângulos
https://www.todamateria.com.br/classificacao-dos-triangulos/
Condição de existência de triângulos
https://mundoeducacao.uol.com.br/matematica/condicao-existencia-um-triangulo.htm




