Triângulos

Não há dúvidas de que o triângulo é uma das figuras mais importantes da geometria (talvez até a mais importante). Mas por quê? Se você viu a página sobre polígonos, viu que podemos dividir alguns dos polígonos regulares em diversos triângulos, ou seja, com apenas uma figura podemos resolver diversos tipos de problemas, o que facilita muito a nossa vida. 

Já que essas figuras são tão importantes assim, que tal conhecer mais sobre elas?

Trigonometria no triângulo retângulo

Como vimos na página sobre o Teorema de Pitágoras, um triângulo retângulo é composto por três partes: o cateto oposto, o cateto adjacente e a hipotenusa. E a partir delas podemos estabelecer as chamadas relações trigonométricas, que são calculadas em relação a um determinado ângulo agudo da figura. As mais importantes são:

• Seno: é a relação obtida pelo quociente do cateto oposto pela hipotenusa, ou seja:

Seno = cateto oposto/hipotenusa

Que pode ser denotado por sen = co/hi

• Cosseno: é a relação obtida pelo quociente do cateto adjacente pela hipotenusa, ou seja:

Cosseno = cateto adjacente/hipotenusa

Que pode ser denotado por cos = ca/hi

• Tangente: é a relação obtida pelo quociente do cateto oposto pelo cateto adjacente, ou seja:

Tangente = cateto oposto/cateto adjacente

Que pode ser denotado por tg = co/ca

Porém, há ainda outra forma de descobrirmos a tangente, e para isso basta fazer o quociente seno/cosseno. Por quê? 

Olha só que interessante, temos que sen = co/hi e cos = ca/hi. Ou seja, na divisão sen/cos, temos:.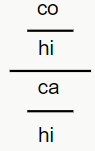 

Resolvendo essa divisão de frações, temos que 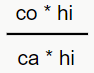. Desse modo, podemos cancelar hi/hi, ficando apenas com co/ca, que é justamente a tangente.

Existem outras relações também, mas elas não são tão importantes quanto as que vimos acima:

• Secante = 1/cosseno

Que pode ser denotado por sec = 1/cos

• Cossecante = 1/seno

Que pode ser denotado por cossec = 1/sen

• Cotangente = cosseno/seno

Que pode ser denotado por cotg = cos/sen

Os ângulos notáveis

Na primeira página deste módulo sobre triângulos, falamos em como classificá-los a partir de seus ângulos. Na trigonometria, ângulos são essenciais, e por isso há os chamados ângulos notáveis, que são os ângulos que aparecem com mais frequência. São eles: 30°, 45° e 60°, e seus valores de seno, cosseno e tangente podem ser encontrados na tabela a seguir:

	30°	45°	60°
Seno
Cosseno
Tangente

Mas lembre-se que todos os ângulos possuem valores de seno, cosseno e tangente. É claro que não precisa lembrar de todos, as tabelas existem para isso, como a disponível em: Tabela Trigonométrica. Dê uma olhada, baixe-a e volte a observá-la sempre que precisar. 😉

Mas para que serve essa tal de trigonometria? Vamos dar uma olhada em algumas aplicações.

Aplicações

1) Medir a distância entre astros: a trigonometria, juntamente com outras técnicas relacionadas aos triângulos, é uma ferramenta importante na astronomia, pois permite que seja possível estimar a distância entre corpos celestes, como por exemplo, a distância da Terra até o Sol.

2) Medir alturas: sabendo a distância horizontal e o ângulo entre o chão e um determinado ponto mais alto, é possível calcular alturas (ou profundidades) que não conseguiríamos medir utilizando simples instrumentos de medida.

3) Construção de rampas e estruturas inclinadas: a utilização da trigonometria é muito útil na construção de rampas e superfícies inclinadas, pois mexer com ângulos é uma das principais funções da trigonometria.

E é isso, acabamos por aqui nosso assunto sobre triângulos, foi bastante conteúdo, mas não poderíamos esperar menos de uma figura tão importante para nós. 🙂

Referências