Juros simples e compostos

Para começar o conteúdo sobre juros, primeiro precisamos defini-lo. O juros é, basicamente, um valor a mais que será pago ou recebido por uma pessoa quando ela realizar uma operação financeira, como empréstimos e financiamentos (onde a pessoa paga juros), ou investimentos (onde a pessoa recebe os juros). No entanto, existem dois tipos de juros, o simples e o composto. Porém, antes de passarmos por cada um deles, é importante dar uma olhada em alguns conceitos importantes.

Conceitos

• Capital (C): é o dinheiro que uma pessoa tem em um determinado momento. 
• Juros (J): é o dinheiro pago ou recebido após uma operação financeira.
• Montante (M): corresponde à soma do capital e do juros (C + J), ou seja, é o valor após a aplicação dos juros.
• Taxa de juros (i): corresponde ao valor, expresso em porcentagem, de quanto será pago ou recebido. A taxa é aplicada sobre o capital, podendo ser cobrada ao ano (a.a), ao mês (a.m) ou ao dia (a.d).

Juros simples

Os juros simples são o tipo de juros que são cobrados sempre em relação ao valor inicial da operação financeira, ou seja, se pegarmos emprestado R$ 10.000,00 com uma taxa de juros de 5% a.a, para pagar em 2 anos, no primeiro ano iremos pagar R$ 500,00 de juros, e no segundo ano iremos pagar… R$ 500,00 de novo, totalizando, ao final, R$ 11.000,00, pois o juros simples é sempre sobre o valor inicial da operação, que nesse caso é R$ 10.000,00.

Para calcular os juros simples, utilizaremos a seguinte fórmula:

Js = C * i * t

Onde Js é o juros, C é o capital inicial, i é a taxa e t é o tempo da operação.

Um ponto importante aqui é que o tempo (t) deve estar sempre na mesma unidade da taxa (i), ou seja, se a taxa é anual, o tempo deve ser escrito em anos, se é mensal, em meses, e se é diária, em dias.

Perceba que, como o cálculo é feito sempre em relação ao valor inicial, então temos que os juros simples crescem de maneira linear e constante, como uma função linear.

Juros composto

Os juros compostos, também chamados de juros sobre juros, são o tipo de juros que são cobrados não sobre o valor inicial, mas sim sobre o valor mais recente da operação financeira, ou seja, o cálculo acontece sobre o montante, e não o valor inicial. Por exemplo, se pegarmos emprestado R$ 10.000,00 com uma taxa de juros de 5% a.a, para pagar em 2 anos, no primeiro ano iremos pagar R$ 500,00 de juros, no entanto, no segundo ano, o cálculo é sobre o montante, ou seja, R$ 10.500,00, resultando em R$ 525,00, totalizando R$ 11.025,00 ao final.

Para calcular os juros compostos, utilizaremos a seguinte fórmula:

Jc = C (1+i)^t

Onde Jc é o juros, C é o capital inicial, i é a taxa e t é o tempo da operação. Assim como nos juros simples, o tempo (t) deve estar sempre na mesma unidade da taxa (i), ou seja, se a taxa é anual, o tempo deve ser escrito em anos, se é mensal, em meses, e se é diária, em dias.

Perceba que esta fórmula é bem parecida com o termo geral da PG (Progressão Geométrica). Desse modo, os juros compostos têm um comportamento exponencial, ou seja, funcionam como uma função exponencial.

Comparação

Você deve ter percebido nas explicações anteriores que o juros simples rende menos que o composto, né? Nos exemplos pode não ter ficado tão claro o quão diferente é o rendimento de um em comparação ao outro. Sendo assim, vamos ver como se comportam os juros simples e compostos graficamente? Para isso, iremos fixar C = 1 e i = 0,5% a.m e deixar o t em aberto.

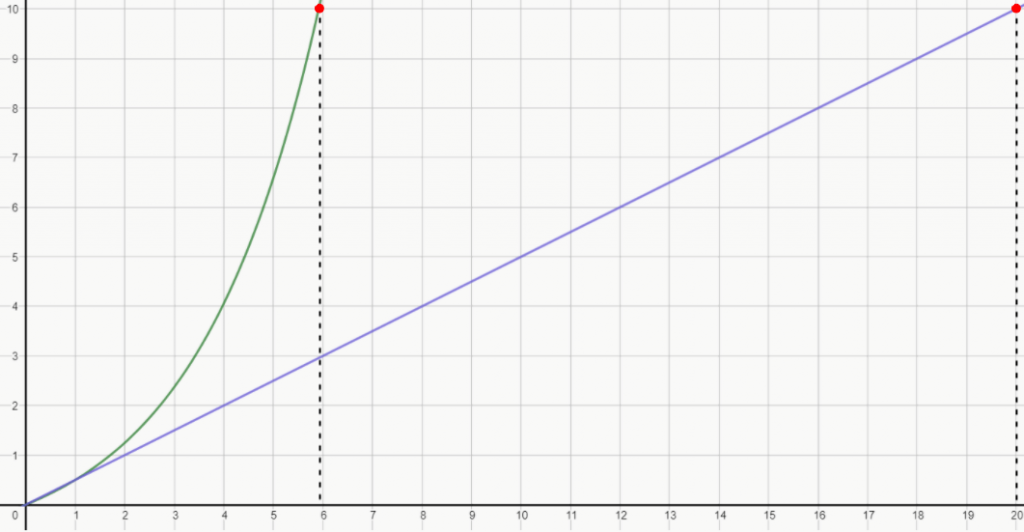
A reta verde representa os juros compostos, enquanto a reta azul representa os juros simples. Perceba que, no início, ambos crescem juntos. No entanto, os juros compostos disparam a partir do segundo mês (eixo x). Enquanto os juros compostos chegam a 10 reais (eixo y) gerados em apenas seis meses, os juros simples demoram vinte meses para alcançar o mesmo valor. E isso se deve ao comportamento exponencial dos juros compostos, que faz com que ele seja muito mais lucrativo que os juros simples.

Referências

Juros simples e compostos (conceitos e fórmulas)