Estatística
A estatística é o campo da matemática responsável pela coleta, organização, análise, interpretação e representação de dados. A ciência, por exemplo, é uma área que utiliza muito a estatística, sendo ela a principal ferramenta para análise de dados.
Mas não é só o cientista que precisa saber de estatística, pois ela é fundamental para que possamos entender e interpretar (corretamente), através de dados, o mundo em que vivemos, evitando, dessa forma, cair em “pegadinhas” ou notícias falsas por aí. Sendo assim, vamos estudar sobre esse campo tão importante.
Selecione aqui o conteúdo que deseja ver!
Medidas de dispersão
As medidas de dispersão são utilizadas para que possamos saber qual o grau de variação dos nossos dados, pois afinal, nenhuma medida é, de fato, exata, já que há diversos fatores que podem influenciar a coleta de dados, como o instrumento utilizado ou a amostra que estamos estudando. São três as medidas de dispersão: a amplitude, a variância e o desvio padrão.
– Amplitude
A amplitude é a mais simples das medidas de dispersão e consiste basicamente na diferença entre o maior e o menor valor de um conjunto de dados. Vemos isso quando assistimos a previsão do tempo e a/o repórter diz que “a amplitude térmica é de ‘x’ graus”. Ou seja, foi pego a maior temperatura do dia e subtraído pela menor temperatura do mesmo dia.
– Variância
A variância é a medida que nos diz o quão distante da média estão os nossos dados. Para calcular a variância, temos que utilizar a seguinte fórmula:
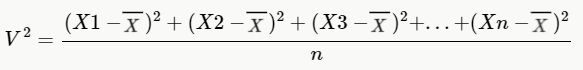
Onde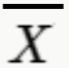 
representa a média dos dados e n a quantidade de dados.
– Desvio padrão
O desvio padrão também representa o quão distante da média estão os nossos dados. Para calculá-lo, temos que utilizar a seguinte fórmula:
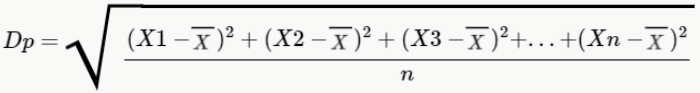
Perceba que esta fórmula é muito parecida com a da variância, pois a única diferença é que temos uma raiz envolvida. Sendo assim, podemos dizer também que o desvio padrão é nada mais nada menos que a raiz quadrada da variância:
Curiosidade: dados, medidas e o erro
Uma outra forma de olhar para o desvio padrão é dizer que ele representa o “erro” (também chamada de incerteza) relacionado aos dados obtidos. Sabe aquela “margem de erro” muito comum em pesquisas de satisfação? É tipo isso. Temos um dado que pode variar em mais (+) ou menos (-) “x” pontos.
Por exemplo, vamos supor que após uma medição, onde encontramos o valor 8 cm, o erro seja de 1 cm. Sendo assim, representamos o dado da seguinte forma:
8 +/- 1 cm
Isso é o que chamamos de erro experimental, que significa que, apesar de termos medido 8, o valor “real” pode ser 7 ou 9. Há ainda uma outra forma de erro, conhecido como erro instrumental, que está associado aos instrumentos de medição (balanças, réguas, provetas, béqueres, etc). Em uma régua, por exemplo, o erro consiste na metade do menor valor da escala desse instrumento, ou seja, se a régua utiliza uma escala de 1 mm, então o erro será de +/- 0,5 mm.
A verdade é que, em nenhum experimento ou pesquisa, os dados são, de fato, reais. 😮 Pode parecer algo chocante, mas isso não quer dizer, nem de longe, que as pesquisas não são confiáveis, ok? Quer dizer apenas que temos que levar em consideração os erros experimentais e instrumentais na hora de analisar os dados obtidos, para que eles sejam ainda mais confiáveis.
Para ficar bem claro como utilizar cada uma dessas medidas, que tal um exemplo? Vamos reproduzir a tabela da página anterior para calculá-las.
| Mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | Out | Nov | Dez |
| Temperatura | 34 | 34 | 33 | 32 | 30 | 29 | 29 | 32 | 34 | 35 | 34 | 34 |
a) Amplitude
Olhando a tabela, vemos que o maior valor presente é o 35, enquanto o menor valor é o 29. Sendo assim, basta subtrair ambos os valores para encontrar a amplitude.
35 – 29 = 6
b) Variância
Na página anterior, vimos que a média dos valores da tabela é igual a 33,5 (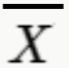). Sabendo disso, podemos utilizar a fórmula da variância. Como temos doze dados, então n = 12.
*Como a fórmula é muito grande, colocaremos apenas os primeiros dois e o último valores. No entanto, o procedimento é o mesmo para qualquer valor, ou seja, subtrair pela média e elevar ao quadrado.
Portanto, a variância é igual a 12,2.
c) Desvio padrão
Como já sabemos quanto vale a variância, o mais simples é tirar a raiz quadrada dela para encontrar o desvio padrão, né?
Desse modo, o desvio padrão é igual a 3,49.
Finalizamos aqui o conteúdo sobre medidas de dispersão. E aí, tá afim de ver uns gráficos? Vá para a próxima página!