Análise Combinatória

A análise combinatória é um campo da matemática que se dedica ao estudo de problemas relacionados à contagem, de modo que o objetivo dessa área é descobrir qual é a quantidade de agrupamentos possíveis em uma determinada situação. Existem diversas aplicações dessa área, e, mesmo sem saber, muitas vezes a utilizamos, como veremos ao longo das páginas.

Dentre os principais tipos de agrupamentos, temos o arranjo, a combinação e a permutação. Mas você sabe qual a diferença entre eles?

Permutação

A permutação é nada mais nada menos que uma troca. No caso da análise combinatória, isso significa que pegamos uma determinada quantidade de elementos e vamos apenas trocando suas posições até encontrarmos todas as configurações (ou sequências) possíveis. Podemos dizer também que a permutação é um caso especial do arranjo, que ocorre quando n é igual a p. 

Existem alguns tipos de permutação, sendo eles: a simples, a com repetição e a circular. Vamos ver como calcular e quando utilizar cada uma delas!

– Permutação simples

Para calcular a permutação simples, utilizamos a seguinte fórmula:

Pn = n!

Onde n = quantidade de elementos de cada conjunto.

Veja como é simples a fórmula da permutação, basta calcular o fatorial de um número. Isso acontece porque estamos apenas pegando uma quantidade n de elementos e trocando suas posições até encontrar todas as sequências possíveis.

– Permutação com repetição

Na permutação com repetição, continuamos com a mesma ideia de pegar uma determinada quantidade de elementos e trocar suas posições para encontrar todas as sequências possíveis. No entanto, agora podemos repetir alguns elementos para formar nossas sequências.

Mas como calcular a permutação com repetição?

Para isso, utilizar a seguinte fórmula:

Onde n = quantidade de elementos de cada conjunto, n1 = quantidade de vezes que um elemento n1 repete, n2 = quantidade de vezes que um elemento n2 repete, e assim por diante até chegar em nn, que é a quantidade de vezes que um elemento nn está sendo repetido na sequência.

– Permutação circular

A permutação circular é bem menos famosa que as anteriores, porém, seu conceito é bem simples. Basicamente, a permutação circular ocorre quando realizamos uma permutação de elementos que formam uma circunferência.

Para entendermos de fato como funciona esse tipo de permutação, vamos pensar no gira-gira, um brinquedo muito legal que serve para… girar. Imaginemos também que, em um parque, quatro crianças resolvem brincar no gira-gira. Sendo assim, de quantas maneiras diferentes as crianças poderiam sentar nos bancos do gira-gira?

A imagem a seguir ilustra essa situação.

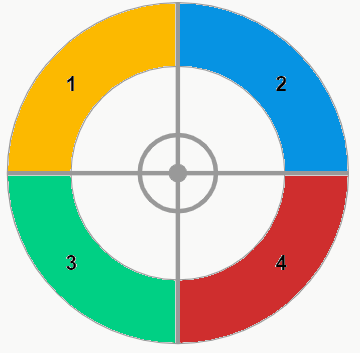
Perceba que, ao girar o gira-gira uma vez, continuamos com a mesma configuração. 

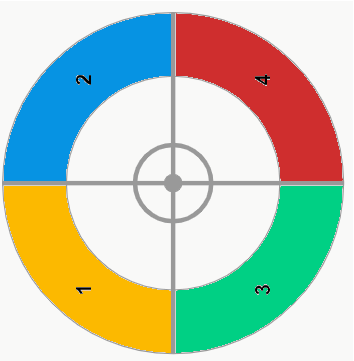
Ao girar duas, três e quatro vezes, também continuamos com a mesma configuração inicial, pois as crianças estão sentadas na mesma posição. Foi o brinquedo que se movimentou.

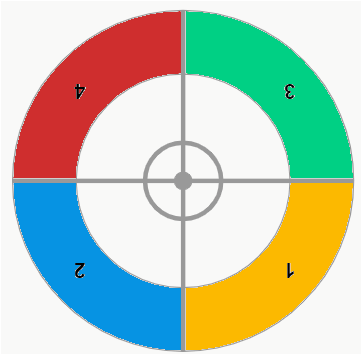
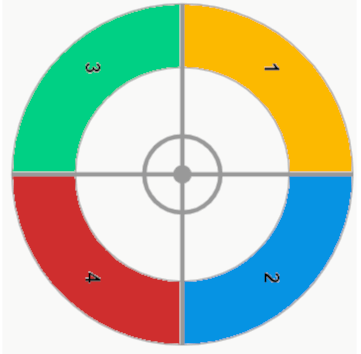
Ou seja, não podemos contar esses 4 casos como sendo configurações diferentes, pois eles são exatamente os mesmos. Sendo assim, perceba que, independente da ordem em que as crianças estão sentadas no brinquedo, teremos sempre 4 casos idênticos. Desse modo, é necessário retirarmos as redundâncias (casos iguais) do valor final.

Para isso, utilizaremos a seguinte fórmula:

Repare que, ao dividir n! por n, estamos retirando os casos iguais da conta. Além disso, dividir por n é o mesmo que fazer (n – 1)!. No caso do nosso exemplo:

ou ainda

Entendeu, não é tão difícil quanto parece, né? Basta nos atentarmos se estamos lidando com uma permutação em algo redondo e aplicar a fórmula.

E é isso, terminamos por aqui o módulo sobre Análise Combinatória!

Referências