Análise Combinatória

A análise combinatória é um campo da matemática que se dedica ao estudo de problemas relacionados à contagem, de modo que o objetivo dessa área é descobrir qual é a quantidade de agrupamentos possíveis em uma determinada situação. Existem diversas aplicações dessa área, e, mesmo sem saber, muitas vezes a utilizamos, como veremos ao longo das páginas.

Dentre os principais tipos de agrupamentos, temos o arranjo, a combinação e a permutação. Mas você sabe qual a diferença entre eles?

Princípio Fundamental da Contagem (P.F.C.)

Para iniciar nossos estudos sobre análise combinatória, precisamos antes falar de um tópico fundamental, que é o Princípio Fundamental da Contagem. Mas, o que diz esse princípio?

De maneira bem simplificada, o Princípio Fundamental da Contagem (ou PFC) nos diz que, dadas duas ou mais situações independentes, podemos encontrar o total de combinações possíveis apenas multiplicando as diferentes opções fornecidas em cada uma.

Vamos ver alguns exemplos?

Ex. 1: Na preparação de uma festa de aniversário surpresa, uma família está na dúvida de qual será o menu da festa. Há 3 opções de salgados (coxinha, esfirra e croquete), 2 opções de bolo (de chocolate e morango), 2 opções de docinhos (brigadeiro e beijinho) e 2 de bebidas (suco e refrigerante). Como a festa é para pouca gente, optou-se por escolher apenas 1 item de cada categoria. Sendo assim, quantos menus é possível criar com as opções disponíveis?

Para encontrar a quantidade de menus possíveis, basta aplicar o PFC, ou seja, temos que multiplicar todas as opções possíveis. Fazendo isso, temos que:

3*2*2*2 = 24 menus diferentes

Ex. 2: Você foi convidado para essa festa de aniversário, e tem que escolher com que roupa ir. Dentre as opções, há 5 camisetas, 3 calças e 3 calçados. Quantos conjuntos é possível formar com essas opções?

Da mesma forma que no exemplo anterior, basta utilizarmos o PFC para descobrir quantos “looks” podemos formar com esses itens. Desse modo, temos que:

5*3*3 = 45 conjuntos diferentes

Viu como é simples? Há ainda uma outra maneira de realizar problemas que envolvam o PFC. Para isso, podemos utilizar o chamado Diagrama de Árvore, que é uma forma visual de representar todas as possíveis combinações de um problema. 

O diagrama pode ser muito útil para problemas onde temos situações com poucas opções. No entanto, para problemas com muitas opções, ele não é muito recomendado, já que pode acabar se tornando muito grande. Em casos assim, é mais fácil fazer a conta.

Vamos refazer o exemplo 1 novamente? Contudo, agora iremos utilizar apenas o Diagrama de Árvore para ficar claro como utilizá-lo.

Ex. 1.1: Vamos resolver o exemplo 1, agora utilizando o diagrama de árvore.

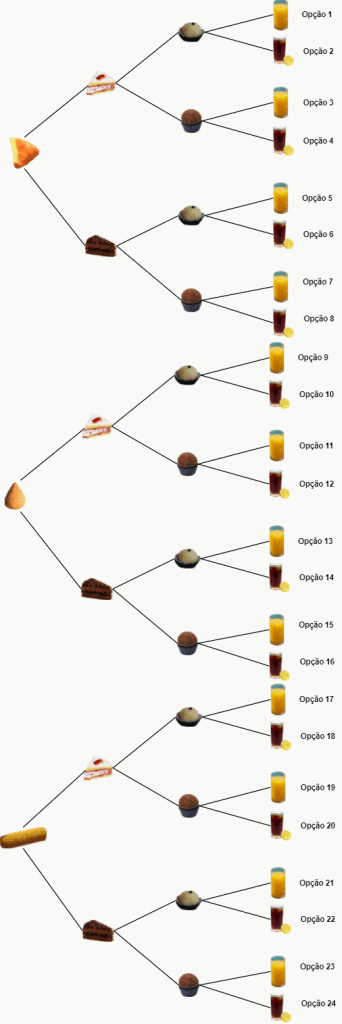
Olha só o tamanho disso… Veja que, feitas todas as relações possíveis, realmente chegamos aos 24 menus diferentes, a diferença é que fizemos isso de uma forma visual. 

Se com 24 opções diferentes já temos um diagrama deste tamanho, imagine só como seria o do exemplo 2, que tem 45! Sendo assim, vamos parar no exemplo 1 mesmo.  

Apesar de o PFC ser muito mais simples e rápido, é sempre bom conhecer diferentes métodos de resolução, pois isso nos ajuda a escolher as melhores estratégias para resolver determinadas situações. Como vimos, o Diagrama de Árvore pode ser útil caso você queira saber quais são as relações, e não somente quantas existem.

 Estamos apenas começando a falar sobre análise combinatória, então vamos lá para mais um tópico. 🙂

Referências

Princípio Fundamental da Contagem

https://mundoeducacao.uol.com.br/matematica/analise-combinatoria.htm

https://www.infoescola.com/matematica/analise-combinatoria/

https://www.todamateria.com.br/principio-fundamental-da-contagem/