Estudo do Ponto e Reta

O estudo do ponto e da reta é fundamental para a geometria, pois esses elementos constituem a base de toda a disciplina. Além disso, podemos utilizá-los para descobrir informações importantes sobre diversas figuras geométricas, como a circunferência, por exemplo.

Distâncias entre…

– Dois pontos

Sabendo quais são as coordenadas de dois pontos, podemos calcular a distância entre eles utilizando a seguinte expressão:

Onde x_a e y_a são as coordenadas de um ponto e x_b e y_b são as coordenadas do outro ponto. No entanto, não precisa se preocupar em decorar isso, pois como os termos estão elevados ao quadrado, não faz diferença quem é quem, já que no fim teremos apenas resultados positivos.

Note que essa fórmula é muito semelhante ao Teorema de Pitágoras, onde d seria a hipotenusa e as coordenadas x e y seriam os catetos de um triângulo retângulo. Vamos ver por quê?

Colocando dois pontos no plano cartesiano, veja que é possível formar um triângulo retângulo.

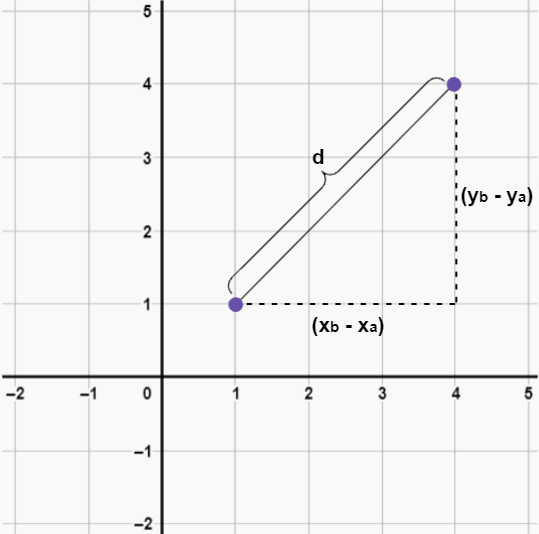
Nesse caso, a hipotenusa é justamente a distância d, e os catetos são as distâncias entre os pontos no eixo x (x_b – x_a) e os pontos no eixo y (y_b– y_a).

Utilizando tudo isso no Teorema de Pitágoras, chegamos à expressão a seguir.

Se você aplicar a raiz quadrada em ambos os lados da expressão, verá que ela é idêntica à expressão inicial 😉.

Curiosidade: a menor distância entre dois pontos é… uma curva geodésica!

Sim, no plano cartesiano, uma reta é realmente a menor distância entre dois pontos, porém, será que isso vale para o planeta Terra? A resposta é: não! E por quê? Simples, porque a Terra não é plana… Desse modo, a forma mais precisa de se calcular distâncias na Terra, nesses casos, é utilizando a curva geodésica.

Essa curva faz parte de uma geometria não vista no Ensino Médio, chamada Geometria Riemanniana, que é diferente da Geometria Euclidiana (a que estudamos no EM), pois, ao invés de trabalhar com retas, ela trabalha com curvas. 

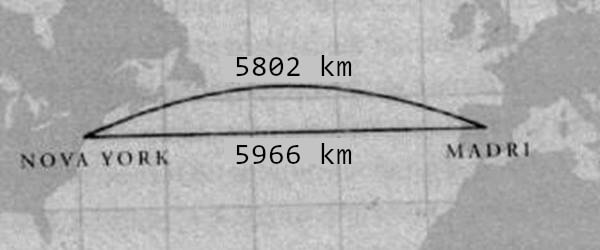
Veja só como seriam as distâncias entre as cidades de Nova York (Estados Unidos) e Madri (Espanha) utilizando uma reta e uma curva geodésica.

Bem interessante, né? Depois desta curiosidade, vamos continuar com o conteúdo.

– Ponto e reta

Para calcular a distância entre um ponto e uma reta, é necessário que tenhamos duas informações: a equação da reta e as coordenadas do ponto. Dessa forma, o cálculo é feito através da seguinte expressão:

Onde a, b e c são os coeficientes da equação da reta, e x e y são as coordenadas do ponto.

Exemplo: dada a equação da reta -5x + y + 3 = 0 e um ponto P = (7, 1), calcule a distância entre esses elementos.

Para começar, temos que identificar os coeficientes a, b e c da equação da reta. Fazendo isso, encontramos que a = -5, b = 1 e c = 3. 

Sabendo disso, agora é só aplicar a fórmula:

Tirando o módulo da equação e resolvendo a raiz, temos que:

Ou seja, a distância entre a reta e o ponto P é 6,1.

– Duas retas concorrentes

Retas concorrentes, como visto na página anterior, são retas que se cruzam e, portanto, possuem um ponto em comum. Desse modo, a distância entre elas é zero. 

– Duas retas paralelas

No caso de retas paralelas, como a distância entre elas é a mesma para todos os pontos que as compõem, concorda que precisamos de apenas um ponto de uma das retas para calcular a distância entre elas? Olha só:

Desse modo, para duas retas paralelas, basta escolher um ponto qualquer de uma delas e utilizar a mesma expressão da distância entre ponto e reta descrita anteriormente.

E finalizamos aqui o estudo sobre ponto e reta!

Referências

Distância entre retas paralelas

https://sabermatematica.com.br/distancia-entre-retas-paralelas.html