Conjuntos

Conjuntos são utilizados para agrupar coisas. Desse modo, o uso desse conceito vai muito além da matemática e pode ser utilizado em diversos momentos de nossas vidas. Mas como?

Diagrama de Venn

Lembra dos diagramas vistos na página anterior? Eles são conhecidos como “Diagramas de Venn” e são utilizados para representar graficamente a relação entre conjuntos. A principal aplicação desse diagrama é quando temos reuniões de conjuntos. Sabe aqueles problemas onde foi feita uma pesquisa em que tantas pessoas disseram utilizar a marca x, tantas a marca y e tantas as duas marcas, que depois te pedem para descobrir quantas pessoas foram entrevistadas? Então, utilizar o Diagrama de Venn em problemas deste tipo podem nos ajudar a resolvê-los de uma forma muito simples.

Sendo assim, vamos resolver algumas questões para ilustrar seu uso:

1) (UFSE) Os senhores A, B e C concorríam à liderança de certo partido político. Para escolher o líder, cada eleitor votou em apenas dois candidatos de sua preferência. Houve 100 votos para A e B, 80 votos para B e C e 20 votos para A e C. Em consequência:

Resolução: vamos utilizar o Diagrama de Venn para resolver o problema.

Primeiro temos que construir o diagrama utilizando as informações do enunciado. Feito isso, temos o seguinte diagrama:

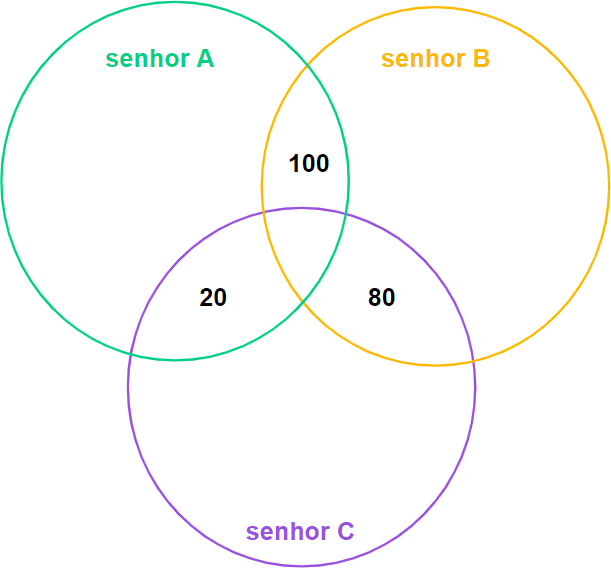
Mas por que os números foram colocados nessas posições? Vamos analisar o diagrama.

Os três círculos possuem pontos de intersecção, que podem ser observados pelas regiões formadas por duas ou mais cores diferentes. O enunciado da questão nos diz que “Houve 100 votos para A e B, 80 votos para B e C e 20 votos para A e C.”. Desse modo, colocamos o 100 na região de intersecção de A e B, o 80 na região de intersecção de B e C, e o 20 na região de intersecção de A e C.

Agora precisamos saber quem venceu a eleição. E como podemos fazer isso? Basta somarmos os valores que estão dentro do conjunto A, os do conjunto B, os do conjunto C e comparar os resultados obtidos.

Fazendo isso: A = 100 + 20 = 120, B = 100 + 80 = 180 e C = 80 + 20 = 100. Comparando os valores, vemos que o conjunto B (senhor B) é o que possui mais votos, e por isso venceu a eleição. Portanto, a alternativa e) é a correta.

Vamos seguir para mais um exemplo.

2) (UNCISAL/2017) Em um supermercado, uma marca de chocolate realizou uma pesquisa sobre as preferências de tipos de chocolate e concluiu que:

I. 24 consumidores gostam de chocolate ao leite;

II. 22 consumidores gostam de chocolate branco;

III. 17 consumidores gostam de chocolate meio amargo;

IV. 5 consumidores gostam de chocolate ao leite e de chocolate meio amargo;

V. 4 consumidores gostam de chocolate meio amargo e de chocolate branco.

Se não houve entrevistado que declarasse preferência pelos chocolates ao leite e branco simultaneamente, qual o número de consumidores consultados?

Resolução: Primeiramente, vamos construir o diagrama com todas as informações que temos.

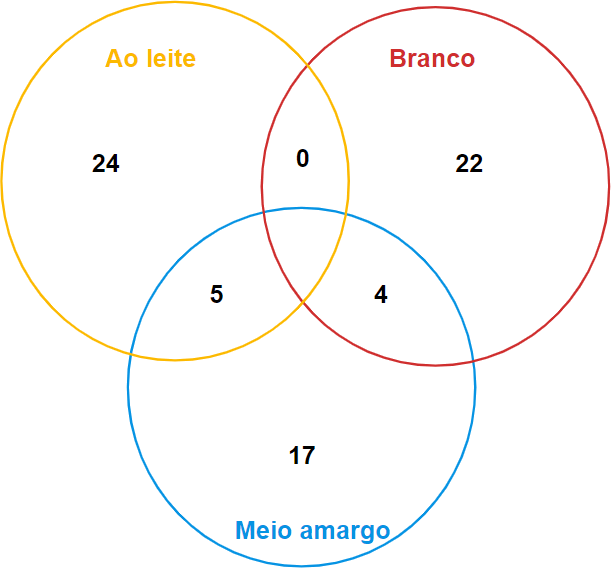
Mas como descobrir quantas pessoas responderam se algumas respostas da pesquisa aparecem em dois conjuntos ao mesmo tempo? A fim de resolver o exercício, nós precisamos descartar respostas duplicadas. E o que são essas “respostas duplicadas”? Pensa comigo, se você fosse um entrevistado e respondesse que gosta de chocolate ao leite e meio amargo, sua resposta iria adicionar 1 “ponto” no grupo do chocolate ao leite, 1 “ponto” ao grupo do chocolate meio amargo e 1 “ponto” na intersecção dos dois, ou seja, a resposta de uma única pessoa contribuiu para o aumento de 3 “pontos” no total de respostas. E por esse motivo é necessário subtrair os valores de cada um dos setores do diagrama. Como assim? Vamos ver a próxima figura.

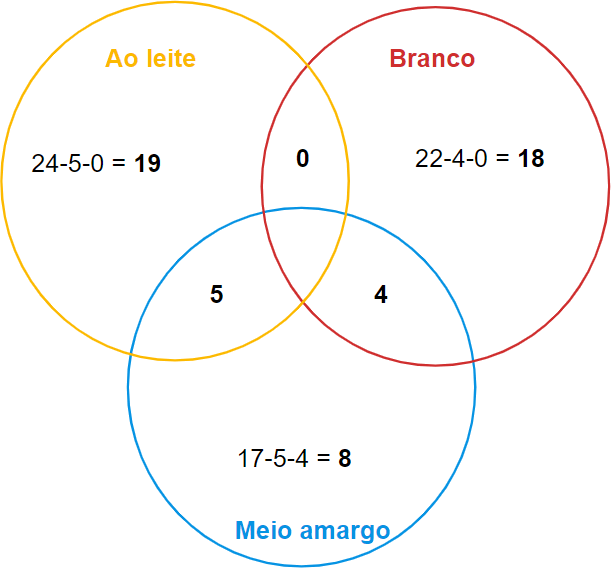
Perceba os valores em negrito. Eles foram obtidos ao subtrair os valores de cada um dos conjuntos dos valores das intersecções. Ao fazer isso, estamos excluindo as duplicidades e podemos encontrar a quantidade real de entrevistados. Para isso, basta somar todos os valores: 19 + 18 + 8 + 5 + 4 = 54. Portanto, a resposta é 54.

Por fim, vamos fazer um exemplo um pouco mais complexo, mas que segue a mesma lógica utilizada até aqui.

3) (UFMG) Em uma pesquisa de opinião, foram obtidos estes dados:

• 40% dos entrevistados leem o jornal A.
• 55% dos entrevistados leem o jornal B.
• 35% dos entrevistados leem o jornal C.
• 12% dos entrevistados leem os jornais A e B.
• 15% dos entrevistados leem os jornais A e C.
• 19% dos entrevistados leem os jornais B e C.
• 7% dos entrevistados leem os três jornais.
• 135 pessoas não leem nenhum dos três jornais.

Considerando-se esses dados, é correto afirmar que o número total de entrevistados é:

Resolução: já sabe, né? Vamos construir o diagrama.

Ao somar todas as porcentagens, você vai ver que dá mais de 100%, ou seja, há duplicidade nas respostas. E como fazemos para excluir essas duplicidades? Isso mesmo, temos que fazer a subtração dos setores onde acontecem as intersecções. Veja que 135 está fora dos conjuntos de pessoas que leem os jornais justamente porque elas não leem nenhum dos três.

Então é só fazer, para o jornal A por exemplo, 40-12-15-7 = 6? Não, temos que tomar um pouco de cuidado aqui, pois devemos primeiramente subtrair as intersecções duplas das triplas, ou seja, pegamos cada um dos setores onde dois jornais se conectam e iremos subtrair do valor presente na posição onde os três se encontram, conforme a figura a seguir:

Os números em negrito são as porcentagem sem as duplicidades geradas pela intersecção tripla. Agora que sabemos os valores de quem respondeu duas revistas somente uma vez, temos que subtrair esses valores da quantidade que lê apenas uma revista, que nem fizemos na questão anterior.

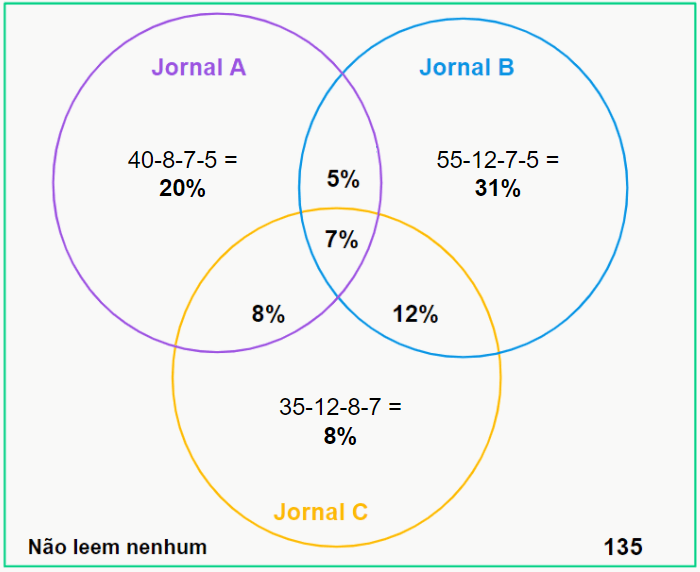
Agora vamos somar todas as porcentagens: 20+31+8+8+12+5+7 = 91%. Portanto, se a quantidade de entrevistados que leem alguma(s) revista(s) é de 91%, isso significa que 135 equivale a 9% do total, certo? Sendo assim, basta fazermos uma regra de três para encontrarmos o total de entrevistados.

Acabou? Ainda não, pois 1365 é igual a 91% do total de entrevistados, falta ainda adicionarmos mais 135, ou seja, 1365+135 = 1500, que é o total de entrevistados na pesquisa. Portanto, a resposta correta é a letra b).

Viu, o Diagrama de Venn deixa tudo mais fácil, basta interpretarmos corretamente o exercício. Com os exemplos vistos aqui, você conseguirá resolver qualquer outro que aparecer, pois a lógica é bem parecida! 

Referências