Circunferência e Círculo
Circunferências e círculos são figuras planas bem comuns no cotidiano. Quem nunca viu um bambolê, um anel, um relógio ou uma roda de bicicleta? Desse modo, é importante saber como diferenciá-las e como calcular algumas informações importantes, como área, perímetro, comprimento de arcos, além de entender como utilizar os ângulos presentes no círculo. É… esse assunto tem mais coisas do que você pensou, né? Vamos estudá-lo então?
Selecione aqui o conteúdo que deseja ver!
Arcos da circunferência
Observe a figura a seguir:
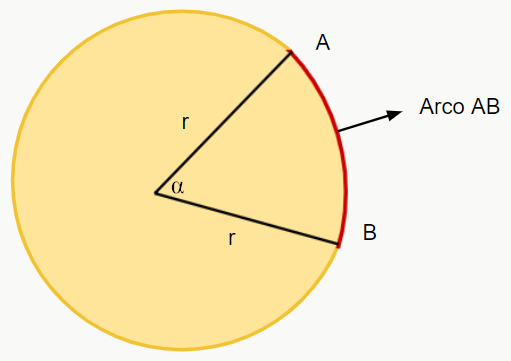
Nela temos o ponto central P, os pontos A e B, que formam uma reta que corresponde ao raio ‘r’, e um ângulo α (alfa). Perceba que as retas formadas pelos pontos A e B dividem a circunferência em dois “pedaços”, e o pedaço entre os pontos A e B é o que chamamos de arco da circunferência. Ou seja, os arcos correspondem a fatias da circunferência formadas por dois pontos. Pense em uma pizza. No começo temos a pizza inteira, mas cada vez que fazemos cortes para retirar os pedaços, estamos construindo diferentes arcos, que são representados pela borda da fatia de pizza retirada. Entendeu?
Mas dá para calcular o comprimento do arco também?
Sim, e podemos fazer ainda mais, como calcular o raio da circunferência e o ângulo do arco. Para isso, temos as seguintes fórmulas:
e
Lembrando que as unidades de arc e r devem ser as mesmas.
Mas qual a diferença entre as duas? A primeira fórmula, que tem 180°, será utilizada quando falarmos de um ângulo alfa medido em graus (°).
Já a segunda fórmula será utilizada quando a medida do ângulo estiver em radianos (rad). Rad… o que?
Radianos é uma outra unidade para medir ângulos. É mais comum utilizarmos graus (°) no dia a dia, mas em muitos momentos pode ser preciso utilizar os radianos (rad). Mas existe alguma relação entre essas duas unidades?
Sim, e é isso que veremos agora.
Graus e radianos
A medida em graus na circunferência ocorre de 0° a 360° (para 1 volta completa). Quando falamos de radianos, temos que a medida varia de 0 a 2π (também para 1 volta completa). Há uma relação entre as duas unidades, e podemos fazer a conversão de uma para outra a qualquer momento, bastando seguir a seguinte regra de três simples:
Vamos ver se isso é verdade? Para tanto, vamos verificar os valores 360° e 2π.
Resolvendo a equação, temos que: 2π*180 = 360*π → 360π = 360π. Portanto, a relação é mesmo verdadeira, pode usar a vontade e sem medo. 🙂
Que tal uns exemplos para finalizarmos essa parte do assunto?
Ex. 1: encontre o comprimento do arco da circunferência de raio 3 cm e arco com ângulo de 45°:
Ex. 2: encontre o comprimento do arco da circunferência de raio 5 cm e arco com ângulo de π/3 radianos:
Ex. 3: vamos converter a) 235° em radianos e b) 6π/5 radianos em graus:
Podemos parar por aí? Até pode, mas é sempre interessante simplificar as frações para trabalharmos com números menores. Para isso, basta dividir o numerador e o denominador pelos mesmos números até chegar a uma forma irredutível.
Fazendo isso, encontramos que 235° = 47π/36 radianos
Um outro modo de fazer essa conversão de radianos para graus é simplesmente substituir π por 180 e realizar as operações, ou seja:
6*180 = 1080
1080/5 = 216°
Que é o mesmo valor encontrado após a regra de 3.
Agora que já sabemos um pouco mais sobre ângulos, podemos continuar nossos estudos. Já ouviu falar de trigonometria? Talvez para o triângulo, mas e para a circunferência? É esse nosso próximo tópico!